题目内容
设a、b是互不相等的正数，则下列不等式中不恒成立的是（ ）
| A、（a+3）2＞2a2+6a+11 | ||||||||
B、
| ||||||||
C、|a-b|+
| ||||||||
D、a2+
|
考点：不等关系与不等式
专题：不等式的解法及应用
分析：本题要找出不等式中不恒成立的选项，必须证明命题的否定是真命题，得到正确选项．
解答：
解：（1）∵（a+3）2-（2a2+6a+11）=a2+6a+9-2a2-6a-11=-a2-2＜0，∴（a+3）2＜2a2+6a+11．
与选项A：（a+3）2＞2a2+6a+11 矛盾，
∴A选项恒不成立．
（2）∵
+
＞
+
，∴
＜
，
∴
＜
，
∴
-
＜
-
．
∴B选项恒成立．
（3）∵a是正数，
∴a+
≥2．
∴a2+
-(a+
)=(a+
)2-(a+
)-2=(a+
+1)(a+
-2)≥0．
∴a2+
≥a+
．
∴D选项恒成立．
（4）当a-b＞0时，|a-b|+
≥2成立，
当a-b＜0时，例如a-b=-1，|a-b|+
=0，|a-b|+
≥2不成立，
∴C选项不恒成立．
故选C．
与选项A：（a+3）2＞2a2+6a+11 矛盾，
∴A选项恒不成立．
（2）∵
| a+3 |
| a+1 |
| a+2 |
| a |
| 1 | ||||
|
| 1 | ||||
|
∴
| ||||
| 2 |
| ||||
| 2 |
∴
| a+3 |
| a+1 |
| a+2 |
| a |
∴B选项恒成立．
（3）∵a是正数，
∴a+
| 1 |
| a |
∴a2+
| 1 |
| a2 |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
∴a2+
| 1 |
| a2 |
| 1 |
| a |
∴D选项恒成立．
（4）当a-b＞0时，|a-b|+
| 1 |
| a-b |
当a-b＜0时，例如a-b=-1，|a-b|+
| 1 |
| a-b |
| 1 |
| a-b |
∴C选项不恒成立．
故选C．
点评：本题考查的是不等关系，通过基本不等式法、作差法、特殊值法比较两式大小，研究不等式是否恒成立，得出本题结论，本题有一定难度，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
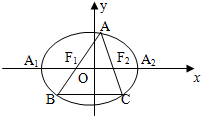如图：A1、A2是椭圆