题目内容
一个袋中装有5个形状大小完全相同的球,其中有2个红球,3个白球.
(Ⅰ)从袋中随机取两个球,求取出的两个球颜色不同的概率;
(Ⅱ)从袋中随机取一个球,将球放回袋中,然后再从袋中随机取一个球,求两次取出的球中至少有一个红球的概率.
(Ⅰ)从袋中随机取两个球,求取出的两个球颜色不同的概率;
(Ⅱ)从袋中随机取一个球,将球放回袋中,然后再从袋中随机取一个球,求两次取出的球中至少有一个红球的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(Ⅰ)所有的取法共有
种,而取出的两个球颜色不同的取法有2×3种,由此求得取出的两个球颜色不同的概率.
(Ⅱ)所有的取法共有5×5种,其中,没有红球的取法有3×3=9种,由此求得求得没有红球的概率,再用1减去此概率,即得所求.
| C | 2 5 |
(Ⅱ)所有的取法共有5×5种,其中,没有红球的取法有3×3=9种,由此求得求得没有红球的概率,再用1减去此概率,即得所求.
解答:
解:(Ⅰ)从袋中随机取两个球,所有的取法共有
=10种,
而取出的两个球颜色不同的取法有2×3=6种,
∴取出的两个球颜色不同的概率为
=
.
(Ⅱ)从袋中随机取一个球,将球放回袋中,然后再从袋中随机取一个球,
所有的取法共有5×5=25种,其中,没有红球的取法有3×3=9种,
故没有红球的概率为
,
故求两次取出的球中至少有一个红球的概率为1-
=
.
| C | 2 5 |
而取出的两个球颜色不同的取法有2×3=6种,
∴取出的两个球颜色不同的概率为
| 6 |
| 10 |
| 3 |
| 5 |
(Ⅱ)从袋中随机取一个球,将球放回袋中,然后再从袋中随机取一个球,
所有的取法共有5×5=25种,其中,没有红球的取法有3×3=9种,
故没有红球的概率为
| 9 |
| 25 |
故求两次取出的球中至少有一个红球的概率为1-
| 9 |
| 25 |
| 16 |
| 25 |
点评:本题主要考查古典概率及其计算公式的应用,对立事件概率间的关系,属于基础题.

练习册系列答案
相关题目
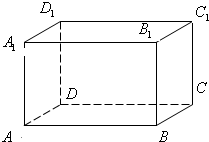 如图,长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长分别为AD=3,AA1=4,AB=5,则从A点沿表面到C1的最短距离为( )
如图,长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长分别为AD=3,AA1=4,AB=5,则从A点沿表面到C1的最短距离为( )A、5
| ||
B、
| ||
C、4
| ||
D、3
|
设f(n)=(
)n-1+(
)n+1(n∈Z),则f(2014)( )
| 1+i |
| 1-i |
| 1-i |
| 1+i |
| A、2 | B、-2 | C、2i | D、-2i |
设l、m是两条不同的直线,α、β是两个不同的平面,则下列正确的是( )
| A、若l⊥α,l⊥β,则α∥β |
| B、若l∥α,α⊥β,则l⊥β |
| C、若l∥m,m∥α,则l∥α |
| D、若α⊥β,α∩β=l,l⊥m,则m⊥α |
