题目内容
设定义在R上的函数f(x)是最小正周期为2π的偶函数,当x∈[0,π]时,0<f(x)<1,且在[0,
]上单调递减,在[
,π]上单调递增,则函数y=f(x)-sinx在[-10π,10π]上的零点个数为( )
| π |
| 2 |
| π |
| 2 |
| A、0 | B、10 | C、20 | D、40 |
考点:函数奇偶性的性质,函数的周期性
专题:函数的性质及应用
分析:把函数y=f(x)-sinx在[-10π,10π]上的零点个数问题,转化为方程f(x)-sinx=0在[-10π,10π]上的根的个数问题,进一步转化为两个函数y=f(x)和y=sinx的交点个数问题,由题目给出的函数y=f(x)的性质作出其大致图象,作出正弦函数的图象,数形结合可得答案.
解答:
解:由函数f(x)是最小正周期为2π的偶函数,得:
函数f(x)的图象关于原点对称,
又由当x∈[0,π]时,0<f(x)<1,
且在[0,
]上单调递减,在[
,π]上单调递增,
可作出函数f(x)图象的大致形状,
求函数y=f(x)-sinx在[-10π,10π]上的零点个数,就是求方程f(x)-sinx=0的根的个数,
即求函数y=f(x)的图象与y=sinx图象交点的个数,如图,
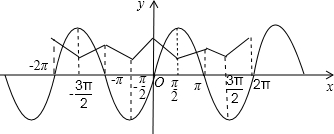
函数y=f(x)的图象与y=sinx的图象交于x轴上方,
以正弦函数[-π,π]为一个周期,也正是函数y=f(x)的一个周期,在每个周期内两个函数图象有两个交点,
区间[-10π,10π]占10个周期长度,
因此在[-10π,10π]上总的交点个数为20个,
所以,函数y=f(x)-sinx在[-10π,10π]上的零点个数为20.
故选:C
函数f(x)的图象关于原点对称,
又由当x∈[0,π]时,0<f(x)<1,
且在[0,
| π |
| 2 |
| π |
| 2 |
可作出函数f(x)图象的大致形状,
求函数y=f(x)-sinx在[-10π,10π]上的零点个数,就是求方程f(x)-sinx=0的根的个数,
即求函数y=f(x)的图象与y=sinx图象交点的个数,如图,

函数y=f(x)的图象与y=sinx的图象交于x轴上方,
以正弦函数[-π,π]为一个周期,也正是函数y=f(x)的一个周期,在每个周期内两个函数图象有两个交点,
区间[-10π,10π]占10个周期长度,
因此在[-10π,10π]上总的交点个数为20个,
所以,函数y=f(x)-sinx在[-10π,10π]上的零点个数为20.
故选:C
点评:本题考查了根的存在性及根的个数的判断,考查了数形结合的解题思想,分析函数零点个数时,有时需要把一个函数的零点问题转化为两个函数图象的交点问题.是基础题.

练习册系列答案
相关题目
如果函数y=f(x-2)是偶函数,那么函数y=f(
x)的图象的一条对称轴是直线( )
| 1 |
| 2 |
| A、x=-4 | ||
| B、x=-2 | ||
C、x=
| ||
D、x=
|
若直线l的倾斜角α满足0°≤α<150°,且α≠90°,则它的斜率k满足( )
A、-
| ||||
B、k>-
| ||||
C、k≥0或k<-
| ||||
D、k≥0或k<-
|
数列1,3,5,7,…的前n项和Sn为( )
| A、n2 |
| B、n2+2 |
| C、n2+1 |
| D、n2+2 |
将正偶数按下表排成4列:

则2000在( )

则2000在( )
| A、第125行,第1列 |
| B、第125行,第2列 |
| C、第250行,第1列 |
| D、第250行,第4列 |
 如图是函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|<
如图是函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|<