题目内容

4．若方程||x|-a2|-a=0有四个不同的实根，则实数a的取值范围为（1，+∞）．

分析 根据绝对值的意义，结合方程||x|-a2|-a=0有四个不同的实根，即可求出实数a的取值范围．

解答 解：方程||x|-a2|-a=0，可得方程||x|-a2|=a，∴a＞0，
∴|x|=a2±a，
∵方程||x|-a2|-a=0有四个不同的实根，
∴a2+a＞0且a2-a＞0，∴a＞1，
故答案为（1，+∞）．

点评 本题考查实数a的取值范围，考查绝对值的意义，正确转化是关键．

练习册系列答案
相关题目
1．运行程序框图，若输出的S的值为$\frac{{{2^9}-1}}{2^9}$，则判断框内的整数a为10．
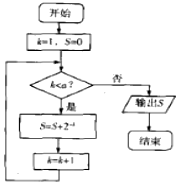
15．如图是一个程序框图，则输出的S的值是（　　）
A．18B．20C．87D．90
12．已知实数集R为全集，A={x|log2（3-x）≤2}，B={x||x-3|≤2}，
（1）求A，B；
（2）求∁R（A∩B）．
19．平面向量$\overrightarrow a$与$\overrightarrow b$的夹角为90°，$\overrightarrow a=（{2，0}），|{\overrightarrow b}|=1$则$|{\overrightarrow a+2\overrightarrow b}|$=2$\sqrt{2}$．
9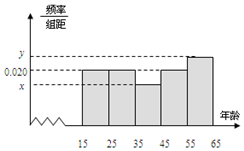．某市文化部门为了了解本市市民对当地地方戏曲是否喜爱，从15-65岁的人群中随机抽样了n人，得到如下的统计表和频率分布直方图．
（Ⅰ）写出其中的a、b及x和y的值；
（Ⅱ）若从第1，2，3组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人，求这三组每组分别抽取多少人？
（Ⅲ）在（Ⅱ）抽取的6人中随机抽取2人，用X表示其中是第3组的人数，求X的分布列和期望．
组号分组喜爱人数喜爱人数
占本组的频率
第1组[15，25）a0.10
第2组[25，35）b0.20
第3组[35，45）60.40
第4组[45，55）120.60
第5组[55，65]c0.80
16．已知$|\overrightarrow a|=1，|\overrightarrow b|=2$且$＜\vec a，\vec b＞=120°$则$|2\overrightarrow a+\overrightarrow b|$等于（　　）
A．4B．12C．2D．2$\sqrt{3}$
13．已知在等比数列{an}中，a5-a1=15，a4-a2=6，则公比q的所有可能的值为$\frac{1}{2}$或2．
14．若?x∈D，总有f（x）＜F（x）＜g（x），则称F（x）为f（x）与g（x）在D上的一个“严格分界函数”．
（1）求证：y=ex是y=1+x和y=1+x+$\frac{{x}^{2}}{2}$在（-1，0）上的一个“严格分界函数”；
（2）函数h（x）=2ex+$\frac{1}{1+x}$-2，若存在最大整数M使得h（x）＞$\frac{M}{10}$在X∈（-1，0）恒成立，求M的值．（e=2.718…是自然对数的底数，$\sqrt{2}$≈1.414，${2}^{\frac{1}{3}}$≈1.260）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网