题目内容
9.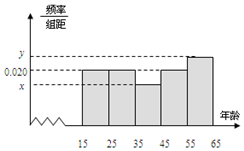 某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.
某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.(Ⅰ)写出其中的a、b及x和y的值;
(Ⅱ)若从第1,2,3组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人,求这三组每组分别抽取多少人?
(Ⅲ)在(Ⅱ)抽取的6人中随机抽取2人,用X表示其中是第3组的人数,求X的分布列和期望.
| 组号 | 分组 | 喜爱人数 | 喜爱人数 占本组的频率 |
| 第1组 | [15,25) | a | 0.10 |
| 第2组 | [25,35) | b | 0.20 |
| 第3组 | [35,45) | 6 | 0.40 |
| 第4组 | [45,55) | 12 | 0.60 |
| 第5组 | [55,65] | c | 0.80 |
分析 (I)由第3组与第4组的人数分别为:$\frac{6}{0.4}$=15,$\frac{12}{0.6}$=20,再根据直方图可知:第1组与第2组的人数都为20人,且抽样总人数n=$\frac{20}{0.02×10}$,可得第5组的人数为100-20-10-15-20.进而定点a,b,c,x,y.
(II)第1,2,3组回答喜欢地方戏曲的人数比为2:4:6=1:2:3,则分层抽样的方法抽取6人,第1组应抽取1人,第2组应抽取2人,第3组应抽取3人.
(III)X可能取的值分别为0,1,2.P(X=0)=$\frac{{∁}_{3}^{2}}{{∁}_{6}^{2}}$,P(X=1)=$\frac{{∁}_{3}^{1}{∁}_{3}^{1}}{{∁}_{6}^{2}}$,P(X=2)=$\frac{{∁}_{3}^{2}}{{∁}_{6}^{2}}$
解答 解:(I)由第3组与第4组的人数分别为:$\frac{6}{0.4}$=15,$\frac{12}{0.6}$=20,
再根据直方图可知:第1组与第2组的人数都为20人,且抽样总人数n=$\frac{20}{0.02×10}$=100,
∴第5组的人数为100-20-10-15-20=25.
且a=0.1×20=2,b=0.2×20=4,c=0.8×25=20.
x=$\frac{\frac{15}{100}}{10}$=0.015,y=$\frac{\frac{25}{100}}{10}$=0.025.
(II)第1,2,3组回答喜欢地方戏曲的人数比为2:4:6=1:2:3,
则分层抽样的方法抽取6人,第1组应抽取1人,第2组应抽取2人,第3组应抽取3人.
(III)X可能取的值分别为0,1,2.P(X=0)=$\frac{{∁}_{3}^{2}}{{∁}_{6}^{2}}$=$\frac{1}{5}$,P(X=1)=$\frac{{∁}_{3}^{1}{∁}_{3}^{1}}{{∁}_{6}^{2}}$=$\frac{3}{5}$,
P(X=2)=$\frac{{∁}_{3}^{2}}{{∁}_{6}^{2}}$=$\frac{1}{5}$,其分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查了频率分布直方图的性质、分层抽样方法、离散型随机变量的分布列与数学期望计算公式,考查了推理能力与计算能力,属于中档题.

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案 某几何体的三视图如图所示,则这个几何体的体积为( )
某几何体的三视图如图所示,则这个几何体的体积为( )| A. | 4 | B. | 8 | C. | $\frac{20}{3}$ | D. | $\frac{26}{3}$ |
| 百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
| 等级 | A | B | C | D |
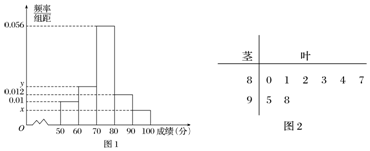
(1)求n和频率分布直方图中x,y的值;
(2)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高一学生中任选3人,求至少有1人成绩是合格等级的概率.
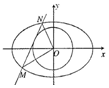 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,短轴长为2,直线l与圆O:x2+y2=$\frac{4}{5}$相切,且与椭圆C相交于M、N两点.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,短轴长为2,直线l与圆O:x2+y2=$\frac{4}{5}$相切,且与椭圆C相交于M、N两点.