题目内容
18.已知$f(x)=\frac{{lnx+{2^x}}}{x^2}$,求f′(1)=2ln2-3.分析 先求导数,再代入计算,即可得出结论.
解答 解:∵$f(x)=\frac{{lnx+{2^x}}}{x^2}$,
∴f′(x)=$\frac{(\frac{1}{x}+{2}^{x}ln2){x}^{2}-(lnx+{2}^{x})•2x}{{x}^{4}}$
∴f′(x)=2ln2-3.
故答案为:2ln2-3
点评 本题考查导数的计算,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
8.设集合M={x|0≤x≤2},N={y|0≤y≤2},从M到N有四种对应如图所示,其中能表示为M到N的函数关系的是( )
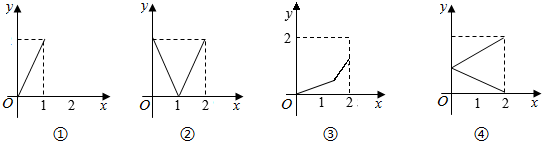

| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
7.设函数f(x)(x∈R)满足f(x+π)=f(x)+sinx,当0≤x<π时,f(x)=0,则$f(\frac{7π}{6})$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |
 已知$x=\frac{π}{6}$是函数$f(x)=({asinx+cosx})cosx-\frac{1}{2}$图象的一条对称轴.
已知$x=\frac{π}{6}$是函数$f(x)=({asinx+cosx})cosx-\frac{1}{2}$图象的一条对称轴.