题目内容
 已知四边形ABCD是空间四边形,E、H分别是AB、AD的中点,F、G分别是边CB、CD上的点,且
已知四边形ABCD是空间四边形,E、H分别是AB、AD的中点,F、G分别是边CB、CD上的点,且| CF |
| CB |
| CG |
| CD |
| 2 |
| 3 |
考点:平行线分线段成比例定理
专题:证明题
分析:由已知中四边形ABCD是空间四边形,E、H分别是AB、AD的中点,由中位线定理可得EH∥BD且EH=
BD;F、G分别是边CB、CD上的点,且
=
=
,由平行线分线段成比例定理,可得FG∥BD,FG=
BD,结合EH∥FG且EH≠FG,易得结论.
| 1 |
| 2 |
| CF |
| CB |
| CG |
| CD |
| 2 |
| 3 |
| 2 |
| 3 |
解答:
证明:∵四边形ABCD是空间四边形,E、H分别是AB、AD的中点,
∴EH为三角形ABD的中位线
∴EH∥BD且EH=
BD
又∵
=
=
,
∴△CFG∽△ABD
且FG∥BD,FG=
BD
∴在四边形EFGH中,EH∥FG
即E,F,G,H四点共面
且EH≠FG
故四边形EFGH是梯形
∴EH为三角形ABD的中位线
∴EH∥BD且EH=
| 1 |
| 2 |
又∵
| CF |
| CB |
| CG |
| CD |
| 2 |
| 3 |
∴△CFG∽△ABD
且FG∥BD,FG=
| 2 |
| 3 |
∴在四边形EFGH中,EH∥FG
即E,F,G,H四点共面
且EH≠FG
故四边形EFGH是梯形
点评:本题考查的知识点是平行线分线段成比例定理,其中根据已知条件,判断出EH∥FG且EH≠FG,是解答本题的关键.

练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
2010年清华大学、中国科学技术大学等五所名校首次进行联合自主招生,同时向一所重点中学的五位学习成绩优秀,并在某些方面有特长的学生发出提前录取通知单.若这五名学生都乐意进这五所大学中的任意一所就读,则仅有两名学生录取到同一所大学(其余三人在其他学校各选一所不同大学)的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若平面区域上的点(x,y)满足不等式
+
≤1.则该平面区域的面积是( )
|
|
| A、30 | B、40 | C、50 | D、60 |
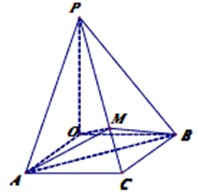 如图,△BCD中,AB=BC=1,∠ACB=120°,O为△ABC的外心,PO⊥平面ABC,且PO=
如图,△BCD中,AB=BC=1,∠ACB=120°,O为△ABC的外心,PO⊥平面ABC,且PO= 设图中的正方体的棱长为a(1)图中哪些棱所在的直线与直线BA1成异面直线?(2)求直线BA1和CC1所成的角的大小.(3)求异面直线BC和AA1的距离.
设图中的正方体的棱长为a(1)图中哪些棱所在的直线与直线BA1成异面直线?(2)求直线BA1和CC1所成的角的大小.(3)求异面直线BC和AA1的距离.