题目内容
5.在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,半圆C的极坐标方程为ρ=4cosθ,θ∈[0,$\frac{π}{2}$].(I)求C的参数方程;
(II)若半圆C与圆D:(x-5)2+(y-$\sqrt{3}$)2=m(m是常数,m>0)相切.试求切点的直角坐标.
分析 (1)利用$\left\{\begin{array}{l}{{ρ}^{2}{=x}^{2}{+y}^{2}}\\{x=ρcosθ}\end{array}\right.$即可得出直角坐标方程,利用cos2t+sin2t=1进而得出参数方程;(2)结合图象和圆的位置关系求出切点的坐标即可.
解答 解:(1)由半圆C的极坐标方程为ρ=4cosθ,θ∈[0,$\frac{π}{2}$],即ρ2=4ρcosθ,
可得C的普通方程为(x-2)2+y2=4(0≤y≤2).
可得C的参数方程为 $\left\{\begin{array}{l}{x=2(1+cost)}\\{y=2sint}\end{array}\right.$(t为参数,0≤t≤π).
(2)如图示: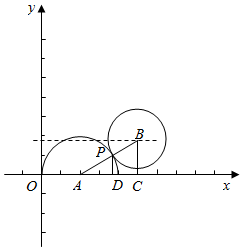
连接圆心AB,则两圆切与P,设P(x,y),
在RT△ABC中,AB=$\sqrt{9+3}$=2$\sqrt{3}$,
∴$\frac{y}{\sqrt{3}}$=$\frac{2}{2\sqrt{3}}$,解得y=1,
∴AD=$\sqrt{3}$,则x=2+$\sqrt{3}$,
∴P(2+$\sqrt{3}$,1).
点评 本题考查了把极坐标方程化为直角坐标方程、参数方程化为普通方程、圆与圆的位置关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
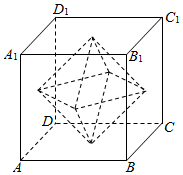 如图所示,用一棱长为a的正方体,制作一以各面中心为顶点的正八面体.求:
如图所示,用一棱长为a的正方体,制作一以各面中心为顶点的正八面体.求: