题目内容
1.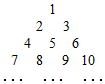 已知数阵:
已知数阵:(1)数阵第i行j列的项为ai,j,求{an,n}的通项公式,并指出2016是第几行第几列的项;
(2)设bn=$\frac{1}{{a}_{n,n}}$,证明:数列{bn}的前n项和Tn<2.
分析 (1)通过观察数列可知an,n=1+2+…n,进而计算可得结论;
(2)通过(1)裂项可知bn=2($\frac{1}{n}$-$\frac{1}{n+1}$),进而并项相加、放缩即得结论.
解答 (1)解:由题意,an,n=1+2+…n=$\frac{n(n+1)}{2}$,
∵$\frac{63(63+1)}{2}$=2016,
∴a63,63=2016,即2016是第63行第63列的项;
(2)证明:由(1)可知bn=$\frac{1}{{a}_{n,n}}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n+1}$),
∴Tn=2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)=2(1-$\frac{1}{n+1}$)<2.
点评 本题考查数列的通项及前n项和,考查裂项相消法,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
10.在△ABC中,若sinAsinBtanC<0,则△ABC( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 锐角或钝角三角形 |
17.已知双曲线mx2+ny2=1(mn<0)的一条渐近线方程为y=2x,此双曲线上的点(x0,y0)满足${y}_{0}^{2}$>4${x}_{0}^{2}$,则该双曲线的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
10.若椭圆上存在三点,使得这三点与椭圆中心恰好是一个正方形的四个顶点,则该椭圆的离心率为( )
| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
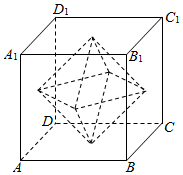 如图所示,用一棱长为a的正方体,制作一以各面中心为顶点的正八面体.求:
如图所示,用一棱长为a的正方体,制作一以各面中心为顶点的正八面体.求: