题目内容
6.△ABC的内角A,B,C所对的边分别为a,b,c,asinB-$\sqrt{3}$bcosA=0.(1)求A;
(2)若a=$\sqrt{21}$,b=4求△ABC的面积.
分析 (1)由已知式子和正弦定理可得$sinAsinB-\sqrt{3}sinBcosA=0$,由三角函数知识可得$tanA=\sqrt{3}$,$A=\frac{π}{3}$;
(2)由余弦定理和已知数据可c的方程,解方程代入面积公式计算可得.
解答 解:(1)∵△ABC中$asinB-\sqrt{3}bcosA=0$,
∴由正弦定理可得$sinAsinB-\sqrt{3}sinBcosA=0$,
又sinB≠0,∴$tanA=\sqrt{3}$,
∵0<A<π,∴$A=\frac{π}{3}$;
(2)由余弦定理可得a2=b2+c2-2bccosA,
把$a=\sqrt{21},b=4$,$A=\frac{π}{3}$代入可得21=16+c2-4c,
整理可得c2-4c-5=0,结合c>0解方程可得c=5,
∴△ABC面积S=$\frac{1}{2}bcsinA=5\sqrt{3}$.
点评 本题考查正余弦定理解三角形,涉及三角形的面积公式,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.汽车4S店是一种以“四位一体”为核心的特许经营模式,包括整车销售、零配件销售、售后服务、信息反馈等.某品汽车4S店为了了解A、B、C三种类型汽车质量问题,对售出的三种类型汽车各取100辆进行跟踪服务,发现各车型一年内需要维修的车辆如下表所示1:
表1
(1)某公司一次性从4S店购买该品牌A、B、C型汽车各一辆,记ξ表示这三辆车的一年内需要维修的车辆数,求ξ的分布列及数学期望(各型汽车维修的频率视为其需要维修的概率);
(2)该品牌汽车4S店为了对厂家新研发的一种产品进行合理定价,将该产品按使事先拟定的各种价格进行试销相等时间,得到数据如表2.
表2
预计在今后的销售中,销量与单价仍然服从$\widehat{y}$=bx+a(b=0.2,a=$\widehat{y}$-b$\widehat{x}$)的关系,且该产品的成本是500元/件,为使4S店获得最大利润(利润=销售收入-成本),该产品的单价应定位多少元.
| 车型 | A型 | B型 | C型 |
| 频数 | 20 | 20 | 40 |
(1)某公司一次性从4S店购买该品牌A、B、C型汽车各一辆,记ξ表示这三辆车的一年内需要维修的车辆数,求ξ的分布列及数学期望(各型汽车维修的频率视为其需要维修的概率);
(2)该品牌汽车4S店为了对厂家新研发的一种产品进行合理定价,将该产品按使事先拟定的各种价格进行试销相等时间,得到数据如表2.
| 单价x(元) | 800 | 820 | 840 | 850 | 880 | 900 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
预计在今后的销售中,销量与单价仍然服从$\widehat{y}$=bx+a(b=0.2,a=$\widehat{y}$-b$\widehat{x}$)的关系,且该产品的成本是500元/件,为使4S店获得最大利润(利润=销售收入-成本),该产品的单价应定位多少元.
11.已知集合A={x|x2<1},B={x|2x<1},则A∩B=( )
| A. | (-1,0) | B. | (-1,1) | C. | (-∞,0] | D. | (-∞,1) |
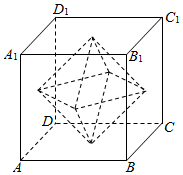 如图所示,用一棱长为a的正方体,制作一以各面中心为顶点的正八面体.求:
如图所示,用一棱长为a的正方体,制作一以各面中心为顶点的正八面体.求: