题目内容
2.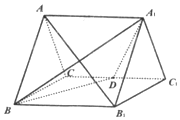 直三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
直三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.(Ⅰ)求证:直线AB1⊥平面A1BD;
(Ⅱ)求二面角A-A1D-B的正弦值;
(Ⅲ)当$\overrightarrow{AE}$=λ$\overrightarrow{A{B}_{1}}$时,异面直线DE和AC所成的角为90°,求CE的长.
分析 (Ⅰ)先证明直线AB1垂直平面A1BD内的两条相交直线BD、A1B,即可证明AB1⊥平面A1BD;
(Ⅱ)设AB1与A1B交于点C,在平面A1BD中,作GF⊥A1D于F,连接AF,说明∠AFG为二面A-A1B-B的平面角,然后求二面角A-A1D-B的大小.
(Ⅲ)取B1C1中点O1,以0为原点,OB,OO1 ,OA 的方向为x、y、z轴的正方向建立空间直角坐标系则B(1,0,0),D(-1,1,0),A1(0,2,$\sqrt{3}$),A(0,0,$\sqrt{3}$),B1(1,2,0),由异面直线DE和AC所成的角为90°,得$\overrightarrow{DE}•\overrightarrow{AC}=0$,λ=2.即∴$\overrightarrow{CE}=\overrightarrow{CA}+\overrightarrow{AE}=(3,4,-\sqrt{3})$,可得CE的长
解答 解:(Ⅰ)取BC中点O,连接AO、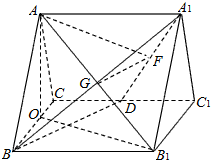 ∵△ABC为正三角形,∴AO⊥BC.
∵△ABC为正三角形,∴AO⊥BC.
∵正三棱柱ABC-A1B1C1中,平面ABC⊥平面BCC1B1,∴AO⊥平面BCC1B1,
连接B1O,在正方形BB1C1C中,O、D分别为BC、CC1的中点,
∴B1O⊥BD,
∴AB1⊥BD.
在正方形ABB1A1中,AB1⊥A1B,
∴AB1⊥平面A1BD.
(Ⅱ)设AB1与A1B交于点G,在平面A1BD中,作GF⊥A1D于F,连接AF,由(Ⅰ)得AB1⊥平面A1BD,
∴∠AFG为二面A-A1D-B的平面角,
在△AA1D中,由等面积法可求得AF=$\frac{4\sqrt{5}}{5}$,
又∵AG=$\frac{1}{2}$=AB1=$\sqrt{2}$,∴sin∠AFG=$\frac{AG}{AF}=\frac{\sqrt{10}}{4}$,
所以二面角A-A1D-B的正弦值:$\frac{\sqrt{10}}{4}$
(Ⅲ):取BC中点O,连接AO.
∵△ABC为正三角形,∴AO⊥BC、
∵正三棱柱ABC-A1B1C1中,平面ABC⊥平面BCC1B1,
∴AO⊥平面BCC1B1,
取B1C1中点O1,以0为原点,OB,OO1 ,OA 的方向为x、y、z轴的正方向建立空间直角坐标系
则B(1,0,0),D(-1,1,0),A1(0,2,$\sqrt{3}$),A(0,0,$\sqrt{3}$),B1(1,2,0),
$\overrightarrow{AE}=\overrightarrow{A{B}_{1}}=(λ,2λ,-\sqrt{3}λ)$,$\overrightarrow{DE}=\overrightarrow{DA}+\overrightarrow{AE}=(λ+1,2λ-1,\sqrt{3}-\sqrt{3}λ)$.$\overrightarrow{AC}=(-1,0,-\sqrt{3})$
∵异面直线DE和AC所成的角为90°,∴$\overrightarrow{DE}•\overrightarrow{AC}=0$,解得λ=2.
即∴$\overrightarrow{CE}=\overrightarrow{CA}+\overrightarrow{AE}=(3,4,-\sqrt{3})$,∴CE的长为$\sqrt{{3}^{2}+{4}^{2}+(-\sqrt{3})^{2}}=2\sqrt{7}$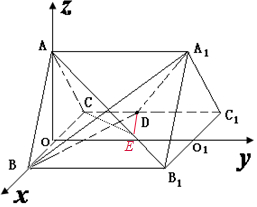
点评 本题考查直线与平面垂直的判定,二面角、异面直线夹角的求法,考查空间想象能力,逻辑思维能力,计算能力,是中档题.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案| A. | 15 | B. | 10 | C. | -15 | D. | -10 |
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
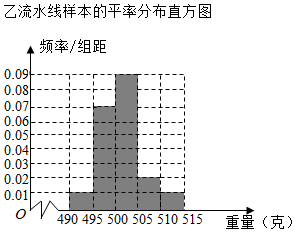 某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在[495,510)内的产品为合格品,否则为不合格品,统计结果如表:
某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在[495,510)内的产品为合格品,否则为不合格品,统计结果如表:甲流水线样本的频数分布表
| 产品重量(克) | 频数 |
| [490,495) | 6 |
| [495,500) | 8 |
| [500,505) | 14 |
| [505,510) | 8 |
| [510,515] | 4 |
(2)从乙流水线上重量值落在[505,515]内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率.
| A. | {1,3,5} | B. | {2,4,6} | C. | {1,5} | D. | {1,6} |