题目内容
2.若a,b∈N,且a+b≤6,复数a+bi共有28个.分析 由题意列举每种情况下复数的个数,相加可得.
解答 解:∵a,b∈N,且a+b≤6,
∴当a=0时,b=0,1,2,3,4,5,6,此时复数共7个;
当a=1时,b=0,1,2,3,4,5,此时复数共6个;
当a=2时,b=0,1,2,3,4,此时复数共5个;
当a=3时,b=0,1,2,3,此时复数共4个;
当a=4时,b=0,1,2,此时复数共3个;
当a=5时,b=0,1,此时复数共2个;
当a=6时,b=0,此时复数共1个;
∴复数a+bi共7+6+5+4+3+2+1=28个
故答案为:28.
点评 本题考查复数的基本概念,由规律列举是解决问题的关键,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.若tanα+cotα=4,则sin2α=( )
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
13.已知数列{an}的前n项和为Sn,且满足an+1=an-an-1(n≥2),a1=1,a2=2,则S2016=( )
| A. | -1 | B. | 0 | C. | 336 | D. | 2016 |
10.若甲、乙、丙三人中,任选两人参加某项活动,甲被选中的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
8.已知双曲线C的焦点为F1,F2,点P是双曲线上任意一点,若双曲线的离心率为2,且|PF1|=2|PF2|,则cos∠PF2F1=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{3}$ |
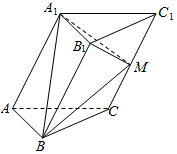 在三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,M为CC1的中点,∠ABC=90°,AC=A1A,∠A1AC=60°,AB=BC=2.
在三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,M为CC1的中点,∠ABC=90°,AC=A1A,∠A1AC=60°,AB=BC=2.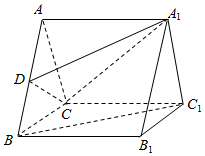 如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形.D为AB中点.
如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形.D为AB中点.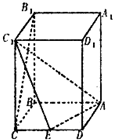 已知四棱柱ABCD-A1B1C1D1,底面ABCD为菱形,∠ADC=60°,BB1⊥底面ABCD,AA1=AC=4,E是CD的中点,
已知四棱柱ABCD-A1B1C1D1,底面ABCD为菱形,∠ADC=60°,BB1⊥底面ABCD,AA1=AC=4,E是CD的中点,