题目内容
16．在等差数列{an}中，前n项和为Sn，若S10=20，S20=30，则S30=30．分析 由等差数列的性质得S10，S20-S10，S30-S20成等差数列，由此能求出S30．
解答 解：∵在等差数列{an}中，前n项和为Sn，S10=20，S20=30，
由等差数列的性质得S10，S20-S10，S30-S20成等差数列，
∴20，10，S30-30成等差数列，
∴2×10=20+S30-30，
解得S30=30．
故答案为：30．
点评 本题考查等差数列的前30项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
7．
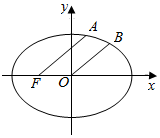如图，已知椭圆方程为$\frac{{x}^{2}}{2}$+y2=1，F是其左焦点，A、B在椭圆上，满足FA∥OB且|FA|：|OB|=3：2，则点A的横坐标为（ ）
如图，已知椭圆方程为$\frac{{x}^{2}}{2}$+y2=1，F是其左焦点，A、B在椭圆上，满足FA∥OB且|FA|：|OB|=3：2，则点A的横坐标为（ ）| A． | 1 | B． | $\frac{3}{4}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
1．
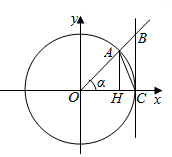如图所示，在单位圆O中，∠AOH=α（0＜α＜$\frac{π}{2}$），若△AOH的面积记为S1，△BOC的面积记为S2，△AOC的面积为S3，扇形AOC的面积记为S4，则（ ）
如图所示，在单位圆O中，∠AOH=α（0＜α＜$\frac{π}{2}$），若△AOH的面积记为S1，△BOC的面积记为S2，△AOC的面积为S3，扇形AOC的面积记为S4，则（ ）| A． | S1=$\frac{1}{2}$sinα | B． | S2=$\frac{1}{2}$tanα | C． | S3=α | D． | S4=$\frac{1}{2}$cosα |