题目内容
5.已知正四棱锥侧面是正三角形,则侧棱与底面所成角为45°.分析 由已知正四菱锥P-ABCD中,所有棱长都相等,设棱长为2,AC∩BD=O,连结PO,PO⊥平面ABCD,∠PDO是侧棱与底面所成角,由此能求出侧棱与底面所成角的大小.
解答  解:由已知正四菱锥P-ABCD中,所有棱长都相等,设棱长为2,
解:由已知正四菱锥P-ABCD中,所有棱长都相等,设棱长为2,
AC∩BD=O,连结PO,PO⊥平面ABCD,
∴∠PDO是侧棱与底面所成角,
则PE=$\sqrt{4-1}$=$\sqrt{3}$,OE=1,PO=$\sqrt{3-1}$=$\sqrt{2}$,
OD=$\frac{1}{2}\sqrt{BD}$=$\frac{1}{2}\sqrt{4+4}$=$\sqrt{2}$,
∴∠PDO=45°.
∴侧棱与底面所成角为45°.
故答案为:45°.
点评 本题考查正四棱锥侧棱与底面所成角的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
17.已知抛物线x2=8y的焦点为F,在抛物线内有一点A(4,4),若该抛物线上存在一动点P,则|PA|+|PF|的最小值为( )
| A. | $4\sqrt{2}+2$ | B. | 4 | C. | $2\sqrt{5}$ | D. | 6 |
 如图,正方形ABCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E.
如图,正方形ABCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E.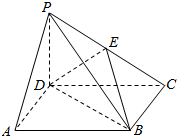 如图,四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.