题目内容
1.若关于x的方程2x3-3x2+a=0在区间[-2,2]上仅有一个实根,则实数a的取值范围为( )| A. | (-4,0]∪[1,28) | B. | [-4,28] | C. | [-4,0)∪(1,28] | D. | (-4,28) |
分析 利用导数求得函数的增区间为[-2 0)、(1,2],减区间为(0,1),根据f(x)在区间[-2,2]上仅有一个零点可得f(0)≠0,故$\left\{\begin{array}{l}{f(-2)=a-28≤0}\\{f(0)=a>0}\\{f(1)=a-1>0}\end{array}\right.$ ①,或$\left\{\begin{array}{l}{f(0)=a<0}\\{f(2)=a+4≥0}\end{array}\right.$②,分别求得①、②的解集,再取并集,即得所求.
解答 解:设f(x)=2x3-3x2+a,则f′(x)=6x2-6x=6x(x-1),x∈[-2,2],
令f′(x)≥0,求得-2≤x≤0,1≤x≤2 令f′(x)<0,求得 0<x<1,
故函数的增区间为[-2 0)、(1,2],减区间为(0,1),
∵若f(1)=0,则a=1,
则f(x)=2x3-3x2+1=(2x+1)(x-1)2,与提意不符合.
∴f(1)≠0
根据f(x)在区间[-2,2]上仅有一个零点,f(-2)=a-28,f(0)=a,f(1)=a-1,f(2)=a+4,
若f(0)=a=0,则f(x)=x2 (2x-3),显然不满足条件,故f(0)≠0.
∴$\left\{\begin{array}{l}{f(-2)=a-28≤0}\\{f(0)=a>0}\\{f(1)=a-1>0}\end{array}\right.$ ①,或$\left\{\begin{array}{l}{f(0)=a<0}\\{f(2)=a+4≥0}\end{array}\right.$②.
解①求得1<a≤28,解②求得-4≤a<0,
故选:C.
点评 本题主要考查方程的根与函数的零点间的关系,利用导数研究函数的单调性,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | $x=\frac{3π}{4}$ | B. | $x=\frac{7π}{6}$ | C. | $x=\frac{7π}{12}$ | D. | $x=\frac{π}{12}$ |
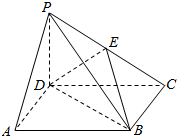 如图,四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.