题目内容

6．若实数x，y满足3x-2y-5=0（1≤x≤3），求$\frac{y}{x}$的最大值和最小值．

分析 通过$\frac{y}{x}$的几何意义，画出3x-2y-5=0（1≤x≤3），直接求出表达式的最值即可．

解答 解：$\frac{y}{x}$的几何意义是：
3x-2y-5=0（1≤x≤3）的图象上的点与坐标原点连线的斜率，
如图：
，
表达式的$\frac{y}{x}$的最大值为：$\frac{2}{3}$．
最小值为：$\frac{-1}{1}$=-1．

点评 本题考查直线的斜率的应用，属于简单的线性规划的应用，考查计算能力．

练习册系列答案
相关题目
16．若函数f（x）=$\sqrt{3}$sin（x+φ）-cos（x+φ）（0＜φ＜π）为奇函数，将函数f（x）图象上所有点横坐标变为原来的一半，纵坐标不变；再向右平移$\frac{π}{8}$个单位得到函数g（x），则g（x）的解析式可以是（　　）
A．$g（x）=2sin（2x-\frac{π}{4}）$B．$g（x）=2sin（2x-\frac{π}{8}）$C．$g（x）=2sin（\frac{1}{2}x-\frac{π}{4}）$D．$g（x）=2sin（\frac{1}{2}x-\frac{π}{16}）$
17．已知圆C过点（1，2）和（2，1），且圆心在直线x+y-4=0上．
（Ⅰ）求圆C的方程；
（Ⅱ）若一束光线l自点A（-3，3）发出，射到x轴上，被x轴反射到圆C上，若反射点为M（a，0），求实数a的取值范围．
14．设f（x）=$\left\{{\begin{array}{l}{{{log}_2}x，}&{x＞0}\\{{2^x}，}&{x≤0}\end{array}}$，则$f（f（\frac{1}{2}））$的值为$\frac{1}{2}$，不等式f（x）＞$\frac{1}{2}$的解集为$（-1，0]∪（\sqrt{2}，+∞）$．
1．已知过球面上三点A，B，C的截面到球心的距离等于球半径的一半，AC=BC=6，AB=4，则球的体积是（　　）
A．$13\sqrt{6}π$B．$27\sqrt{6}π$C．27$\sqrt{7}$πD．7$\sqrt{6}$π
11．不等式$\frac{1}{x-1}$≥-1的解集为（　　）
A．（-∞，0]∪（1，+∞）B．（-∞，0）∪[1，+∞）C．（0，1]D．[0，1）
18．等差数列{an}的前n项和为Sn，若a1+a9+a11=30，则S13=130．
15．函数y=lg（4-2x）的定义域是（　　）
A．（2，4）B．（2，+∞）C．（0，2）D．（-∞，2）
16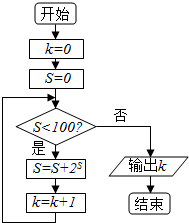．如果执行如图所示的程序，那么输出的值k=（　　）
A．3B．4C．5D．6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网