题目内容
1.已知过球面上三点A,B,C的截面到球心的距离等于球半径的一半,AC=BC=6,AB=4,则球的体积是( )| A. | $13\sqrt{6}π$ | B. | $27\sqrt{6}π$ | C. | 27$\sqrt{7}$π | D. | 7$\sqrt{6}$π |
分析 设出球的半径,小圆半径,通过已知条件求出球的半径,即可求球的体积.
解答 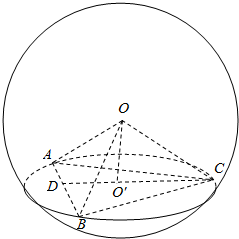 解:如图,设球的半径为r,O′是△ABC的外心,外接圆半径为R,
解:如图,设球的半径为r,O′是△ABC的外心,外接圆半径为R,
则OO′⊥面ABC.在Rt△ACD中,cosA=$\frac{1}{3}$,则sinA=$\frac{2\sqrt{2}}{3}$,
在△ABC中,由正弦定理得$\frac{6}{sinA}$=2R,R=$\frac{9\sqrt{2}}{4}$,即O′C=$\frac{9\sqrt{2}}{4}$.
在Rt△OCO′中,由题意得r2-$\frac{1}{4}$r2=($\frac{9\sqrt{2}}{4}$)2,得r=$\frac{3\sqrt{6}}{2}$.
球的体积=$\frac{4}{3}$πr3=27$\sqrt{6}$π.
故选:B.
点评 本题考查球的体积的求法以及正弦定理的应用,考查学生分析问题解决问题能力,空间想象能力.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
11.已知Πn是正项等比数列{an}的前n项积,且满足a7>1,a8<1,则下列结论正确的是( )
| A. | Π7<Π8 | B. | Π15<Π16 | C. | Π13>1 | D. | Π14>1 |
12.记等差数列的前n项和为Sn,若S3=6,S5=25,则该数列的公差d=( )
| A. | 2 | B. | 3 | C. | 6 | D. | 7 |
13.已知函数f(x)=$\frac{{4}^{x}}{{4}^{x}+2}$,则f($\frac{1}{11}$)+f($\frac{2}{11}$)+…+f($\frac{10}{11}$)的值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
10.下列分别为集合A到集合B的对应:其中,是从A到B的映射的是( )


| A. | (1)(2) | B. | (1)(2)( 3) | C. | (1)(2)(4) | D. | (1)(2)(3)(4) |