题目内容
8．已知集合A={（x，y）|x2+mx-y+2=0，x∈R}，B={（x，y）|x-y+1=0，x∈R}，若A∩B≠∅，求实数m的取值范围．分析 由A与B中方程消去y得到关于x的一元二次方程，根据两集合交集不为空集得到根的判别式大于等于0，求出m的范围即可．
解答 解：由A∩B≠∅，可知，方程x2+mx-y+2=0①与x-y+1=0②有公共解，
①-②得：x2+（m-1）x+1=0，此时△=（m-1）2-4≥0，
解得：m≤-1或x≥3，
则实数m的取值范围是{x|m≤-1或x≥3}．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
18．
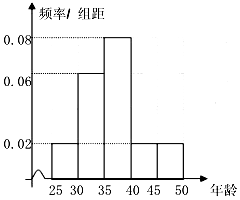我校名教师参加我县“六城”同创“干部职工进网络，服务群众进社区”活动，他们的年龄均在25岁至50岁之间，按年龄分组：第一组[25，30），第二组[30，35），第三组[35，40），第四组[40，45），第五组[45，50]，得到的频率分布直方图如图所示：
如表是年龄的频数分布表．
（1）求正整数a，b，N的值；
（2）根据频率分布直方图估计我校这N名教师年龄的中位数和平均数；
（3）从第一、二组用分层抽样的方法抽取4人，现在从这4人中任取两人接受咸丰电视台的采访，求从这4人中选取的两人年龄均在第二组的概率．
我校名教师参加我县“六城”同创“干部职工进网络，服务群众进社区”活动，他们的年龄均在25岁至50岁之间，按年龄分组：第一组[25，30），第二组[30，35），第三组[35，40），第四组[40，45），第五组[45，50]，得到的频率分布直方图如图所示：| 区间 | [25，30） | [30，35） | [35，40） | [40，45） | [45，50] |
| 人数 | 5 | a | b |
（1）求正整数a，b，N的值；
（2）根据频率分布直方图估计我校这N名教师年龄的中位数和平均数；
（3）从第一、二组用分层抽样的方法抽取4人，现在从这4人中任取两人接受咸丰电视台的采访，求从这4人中选取的两人年龄均在第二组的概率．
已知奇函数$f（x）=\left\{{\begin{array}{l}{-{x^2}+2x}\\ 0\\{{x^2}+2x}\end{array}\begin{array}{l}{（{x＞0}）}\\{（{x=0}）}\\{（{x＜0}）}\end{array}}\right.$
13．命题“任意x∈R，|x|+x2≥0”的否定是（ ）
| A． | 任意x∈R，|x|+x2＜0 | B． | 存在x∈R，|x|+x2≤0 | ||
| C． | 存在x0∈R，|x0|+x02＜0 | D． | 存在x0∈R，|x0|+x02≥0 |
20．集合A={y|y=x-2}，B={y|y=$\sqrt{x}$}，则x∈A是x∈B的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 不充分不必要条件 |
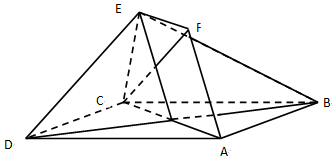（文）如图，正方形ABCD和四边形ACEF所在的平面互相垂直，CE⊥AC，EF∥AC，EF=CE，AB=$\sqrt{2}$EF．