题目内容
在△ABC中,a=10,c-b=8,则
= .
tan
| ||
tan
|
考点:正弦定理,三角函数的化简求值
专题:解三角形
分析:已知两等式相除得到
=
,利用正弦定理化简,再利用和差化积公式及二倍角的正弦函数公式化简,约分后两边展开,利用同角三角函数间基本关系整理即可求出原式的值.
| c-b |
| a |
| 4 |
| 5 |
解答:
解:∵c-b=8,a=10,
∴
=
=
,
利用正弦定理化简得:
=
,即
=
,
整理得:
=
=
,
即5(sin
cos
-cos
sin
)=4(sin
cos
+cos
sin
),
整理得:sin
cos
=9sin
cos
,
两边除以cos
cos
得:tan
=9tan
,
则
=
.
故答案为:
∴
| c-b |
| a |
| 8 |
| 10 |
| 4 |
| 5 |
利用正弦定理化简得:
| sinC-sinB |
| sinA |
| 4 |
| 5 |
| sinC-sinB |
| sin(B+C) |
| 4 |
| 5 |
整理得:
2cos
| ||||
2sin
|
sin
| ||
sin
|
| 4 |
| 5 |
即5(sin
| C |
| 2 |
| B |
| 2 |
| C |
| 2 |
| B |
| 2 |
| B |
| 2 |
| C |
| 2 |
| B |
| 2 |
| C |
| 2 |
整理得:sin
| C |
| 2 |
| B |
| 2 |
| B |
| 2 |
| C |
| 2 |
两边除以cos
| B |
| 2 |
| C |
| 2 |
| C |
| 2 |
| B |
| 2 |
则
tan
| ||
tan
|
| 1 |
| 9 |
故答案为:
| 1 |
| 9 |
点评:此题考查了正弦定理,同角三角函数间的基本关系,熟练掌握正弦定理是解本题的关键.

练习册系列答案
相关题目
命题“若x>0,则x2>0”的否命题是( )
| A、若x>0,则x2≤0 |
| B、若x2>0,则x>0 |
| C、若x≤0,则x2≤0 |
| D、若x2≤0,则x≤0 |
函数f(x)=
+lg(3x+1)的定义域是( )
| 3x2 | ||
|
A、(-
| ||||
B、(-∞,-
| ||||
C、(-
| ||||
D、(-
|
我们把复数a-bi叫做复数z=a+bi(a,b∈R)的共轭复数,记作
,若i是虚数单位,z=1+i,
为复数z的共轭复数,则z•
+|
|-1=( )
. |
| z |
| • |
| z |
| • |
| z |
| • |
| z |
A、
| ||
B、
| ||
C、2
| ||
D、2
|
已知tanα=3,则
=( )
cos(
| ||
| 2sin(π-α)+cosα |
A、-
| ||||
| B、0 | ||||
C、
| ||||
D、
|
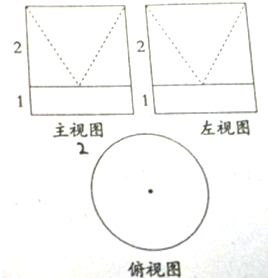 如图是无上底的几何体的三视图,其中正视图和侧视图是全等的图形,外边界是矩形,它的底边长为4,宽为3,俯视图是半径为2的圆,求该几何体的表面积和体积.
如图是无上底的几何体的三视图,其中正视图和侧视图是全等的图形,外边界是矩形,它的底边长为4,宽为3,俯视图是半径为2的圆,求该几何体的表面积和体积.