题目内容
已知tanα=3,则
=( )
cos(
| ||
| 2sin(π-α)+cosα |
A、-
| ||||
| B、0 | ||||
C、
| ||||
D、
|
考点:同角三角函数基本关系的运用,运用诱导公式化简求值
专题:三角函数的求值
分析:原式利用诱导公式及同角三角函数间的基本关系化简,把tanα的值代入计算即可求出值.
解答:
解:∵tanα=3,
∴原式=
=
=
=
,
故选:C.
∴原式=
| sinα-2cosα |
| 2sinα+cosα |
| tanα-2 |
| 2tanα+1 |
| 3-2 |
| 6+1 |
| 1 |
| 7 |
故选:C.
点评:此题考查了同角三角函数基本关系的运用,以及运用诱导公式化简求值,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
已知O是平面上任意一点,且
=
(
+
),则点C是AB的( )
| OC |
| 1 |
| 2 |
| OA |
| OB |
| A、三等分点 | B、中点 |
| C、四等分点 | D、无法判断 |
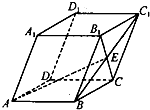 如图,在平行六面体ABCD-A1B1C1D1中,E为BC1与B1C的交点,记
如图,在平行六面体ABCD-A1B1C1D1中,E为BC1与B1C的交点,记| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| AE |
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|