题目内容
3.某几何体的三视图如图所示,则该几何体的体积为( )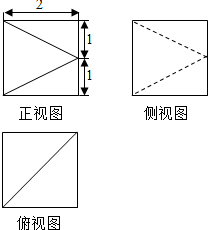
| A. | 6 | B. | $\frac{16}{3}$ | C. | $\frac{20}{3}$ | D. | $\frac{22}{3}$ |
分析 根据几何体的三视图,得出该几何体是棱长为2的正方体,去掉两个三棱锥所剩的部分,结合图中数据求出它的体积.
解答 解:根据几何体是三视图,得;
该几何体是一棱长为2的正方体,去掉两个三棱锥所剩的部分,如图所示;
所以该几何体的体积为23-2×$\frac{1}{3}$×$\frac{1}{2}$×22×1=$\frac{20}{3}$.
故选:C.
点评 本题考查了利用三视图求几何体的体积的应用问题,解题的关键是根据三视图还原出几何体的结构特征,是基础题.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
15.直线ax+by-a-b=0(a≠)与圆x2+y2-2=0的位置关系为( )
| A. | 相离 | B. | 相切 | C. | 相交或相切 | D. | 相交 |
12.如图,是圆锥一部分和四分之一球组成的组合体的三视图,则此几何体的体积为( )
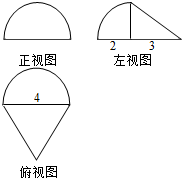

| A. | $\frac{8π}{3}$ | B. | $\frac{16π}{3}$ | C. | $\frac{14π}{3}$ | D. | $\frac{2π}{3}$ |
13.某几何体的三视图如图所示.则该几何体的外接球的表面积为( )


| A. | 8π | B. | 16π | C. | 32π | D. | 64π |
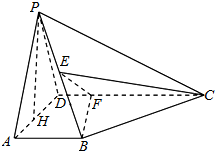 如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,E是PB的中点,F是CD上的点,PH为△PAD中AD边上的高.
如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,E是PB的中点,F是CD上的点,PH为△PAD中AD边上的高.