题目内容
1.已知平面向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$满足$\overrightarrow{OA}•\overrightarrow{OB}=0$,且$|{\overrightarrow{OA}}|=|{\overrightarrow{OC}}|=1$,$|{\overrightarrow{OB}}|=\sqrt{3}$,则$\overrightarrow{CA}•\overrightarrow{CB}$的最大值是3.分析 建立平面直角坐标系,设出A,B,C坐标,表示出$\overrightarrow{CA},\overrightarrow{CB}$的坐标,得出数量积的表达式,求出最值.
解答 解:∵$\overrightarrow{OA}•\overrightarrow{OB}=0$,∴$\overrightarrow{OA}⊥\overrightarrow{OB}$,设A(1,0),B(0,$\sqrt{3}$),C(cosθ,sinθ),
∴$\overrightarrow{CA}$=(1-cosθ,-sinθ),$\overrightarrow{CB}$=(-cosθ,$\sqrt{3}$-sinθ),
∴$\overrightarrow{CA}•\overrightarrow{CB}$=-(1-cosθ)cosθ-sinθ($\sqrt{3}$-sinθ)=sin2θ+cos2θ-cosθ-$\sqrt{3}$sinθ=1-2sin(θ+$\frac{π}{6}$).
∴当sin(θ+$\frac{π}{6}$)=-1时,$\overrightarrow{CA}•\overrightarrow{CB}$取得最大值3.
故答案为:3.
点评 本题考查了平面向量的数量积运算,使用坐标法可使计算简单.

练习册系列答案
相关题目
11.过点(1,-2)的抛物线的标准方程是( )
| A. | y2=4x或x2=$\frac{1}{2}$y | B. | y2=4x | C. | y2=4x或x2=-$\frac{1}{2}$y | D. | x2=-$\frac{1}{2}$y |
16.甲、乙、丙、丁四人排成一排,其中甲、乙两人相邻的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
11.在△ABC中,a=5,b=4,C=60°,则$\overrightarrow{CB}$•$\overrightarrow{CA}$的值为( )
| A. | -10 | B. | 10 | C. | -10$\sqrt{3}$ | D. | 10$\sqrt{3}$ |
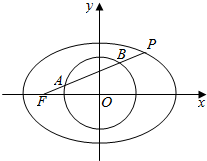 如图,过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F作直线与圆x2+y2=$\frac{{a}^{2}}{4}$及椭圆依次交于点A、B、P,若FA=PB,且AB=$\frac{\sqrt{3}a}{2}$,则椭圆的离心率为$\frac{\sqrt{10}}{4}$.
如图,过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F作直线与圆x2+y2=$\frac{{a}^{2}}{4}$及椭圆依次交于点A、B、P,若FA=PB,且AB=$\frac{\sqrt{3}a}{2}$,则椭圆的离心率为$\frac{\sqrt{10}}{4}$. 如图,有一块平行四边形绿地ABCD,经测量BC=2百米,CD=1百米,∠BCD=120°,拟过线段BC上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将绿地分为面积之比为1:3的左右两部分,分别种植不同的花卉,设EC=x百米,EF=y百米.
如图,有一块平行四边形绿地ABCD,经测量BC=2百米,CD=1百米,∠BCD=120°,拟过线段BC上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将绿地分为面积之比为1:3的左右两部分,分别种植不同的花卉,设EC=x百米,EF=y百米.