题目内容
9.若复数z满足$|{\begin{array}{l}1&i\\{1-2i}&z\end{array}}|=0$(i为虚数单位),则|z|=$\sqrt{5}$.分析 利用行列式的性质可得z-i(1-2i)=0,再利用复数的运算法则、模的计算公式即可得出.
解答 解:∵复数z满足$|{\begin{array}{l}1&i\\{1-2i}&z\end{array}}|=0$(i为虚数单位),
∴z-i(1-2i)=0,
化为z=i+2.
则|z|=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题考查了行列式的性质、复数的运算法则、模的计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.已知双曲线C:$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{{m}^{2}}$=1的左右焦点分别为F1,F2,双曲线外一点P关于点F1、F2的对称点分别为A、B,线段PQ的中点在曲线C上,则|QA|-|QB|的值为( )
| A. | 6 | B. | 12 | C. | 24 | D. | 4|m| |
14.如果a>b>0,那么下列不等式中不正确的是( )
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | $\frac{1}{a}>\frac{1}{b}$ | C. | ab>b2 | D. | a2>ab |
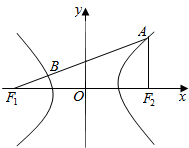 已知双曲线中心在原点,焦点在x轴上,过左焦点F1作倾斜角为30°的直线l,交双曲线于A,B两点,F2为双曲线的右焦点,且AF2⊥x轴,如图.
已知双曲线中心在原点,焦点在x轴上,过左焦点F1作倾斜角为30°的直线l,交双曲线于A,B两点,F2为双曲线的右焦点,且AF2⊥x轴,如图.