题目内容
15．已知函数f（x）=$\left\{\begin{array}{l}{（\frac{1}{2}）^{x}，x≥1}\\{lo{g}_{4}x，0＜x＜1}\end{array}\right.$则f（f（2））=-1．分析 先求出f（2）=（$\frac{1}{2}$）2=$\frac{1}{4}$，从而f（f（2））=f（$\frac{1}{4}$）=$lo{g}_{4}\frac{1}{4}$，由此能求出结果．
解答 解：∵函数f（x）=$\left\{\begin{array}{l}{（\frac{1}{2}）^{x}，x≥1}\\{lo{g}_{4}x，0＜x＜1}\end{array}\right.$，
∴f（2）=（$\frac{1}{2}$）2=$\frac{1}{4}$，
f（f（2））=f（$\frac{1}{4}$）=$lo{g}_{4}\frac{1}{4}$=-1．
故答案为：-1．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
11．执行如图所示的程序框图，若输入的a，b分别为36，28，则输出的a=（ ）
| A． | 4 | B． | 8 | C． | 12 | D． | 20 |
3．甲、乙两人相约周六上午8：00到8：30之间在公交车站乘车去新华书店，先到者若等了15分钟还没有等到对方，则需发微信联系．假设两人的出发时间是独立的，在8：00到8：30之间到达车站的时间是等可能的，则两人不需要发微信联系就能见面的概率是（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
20．若复数z满足$\frac{3+4i}{i}$=$\frac{z}{1+i}$，则z等于（ ）
| A． | 7+i | B． | 7-i | C． | 7+7i | D． | -7+7i |
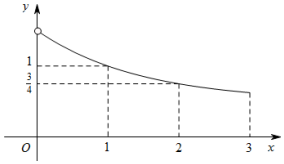已知函数f（x）是定义在[-3，0）∪（0，3]上的奇函数，当x∈（0，3]时，f（x）的图象如图所示，那么满足不等式f（x）≥2x-1 的x的取值范围是[-3，-2]∪[0，1]．