题目内容
已知点A（0，1，0）、B（-1，0，-1）、C（2，1，1），若点P（x，0，z）满足PA⊥AB，PA⊥AC，试求点P的坐标．
考点：空间中的点的坐标,向量的数量积判断向量的共线与垂直
专题：空间向量及应用
分析：利用PA⊥AB，PA⊥AC，得到向量的数量积为0．求解即可．
解答：
解：∵PA⊥AB，PA⊥AC，
∴
•
=0，
•
=0．
∴
，解得
．
∴P（
，0，--
）．
∴
| PA |
| AB |
| PA |
| AC |
∴
|
|
∴P（
| 1 |
| 3 |
| 2 |
| 3 |
点评：本题考查空间向量数量积的应用，熟练正确向量垂直与数量积是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
函数f（x）=（x+1）|log2x|-1的零点个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
若2°的圆心角所对的弧长为2m，那么这个弧所在圆的面积为（ ）
A、
| ||
B、
| ||
C、（
| ||
D、
|
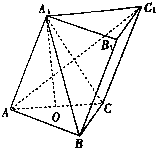如图，在斜三棱柱ABC-A1B1C1中，点A1在底面ABC上的射影O是AC的中点，BC⊥AC，四边形BCC1B1是菱形，直线AB与平面ACC1A1所成的角为45°．