题目内容
8．已知两条直线a，b和平面α，若a⊥b，b?α，则“a⊥α”是“b∥α”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 分别判断出充分性和不必要性即可．
解答 解：若a⊥b，b?α，a⊥α，则b∥α，是充分条件，
若a⊥b，b?α，b∥α，推不出a⊥α，不是必要条件，
则“a⊥α”是“b∥α”的充分不必要条件，
故选：A．
点评 本题考查了充分必要条件，考查线面、线线的位置关系，是一道基础题．
练习册系列答案
相关题目
12．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象过点P（$\frac{π}{12}$，0），图象上与点P最近的一个最高点是Q（$\frac{π}{3}$，5），则函数f（x）的一个单调递增区间为（ ）
| A． | [-$\frac{π}{3}$，$\frac{π}{3}$] | B． | [-$\frac{π}{4}$，$\frac{π}{2}$] | C． | [-$\frac{π}{3}$，$\frac{π}{6}$] | D． | [0，$\frac{π}{3}$] |
19．模拟考试后，某校对甲、乙两个班的数学考试成绩进行分析，规定：不少于120分为优秀，否则为非优秀，统计成绩后，得到如下的2×2列联表，已知在甲、乙两个班全部100人中随机抽取1人为优秀的概率为$\frac{3}{10}$．
（1）请完成上面的2×2列联表
（2）根据列联表的数据，若按97.5%的可靠性要求，能否认为“成绩与班级有关系”？
（3）在“优秀”的学生人中，用分层抽样的方法抽取6人，再平均分成两组进行深入交流，求第一组中甲班学生恰有2人的概率．
参考公式与临界表：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 100 |
（2）根据列联表的数据，若按97.5%的可靠性要求，能否认为“成绩与班级有关系”？
（3）在“优秀”的学生人中，用分层抽样的方法抽取6人，再平均分成两组进行深入交流，求第一组中甲班学生恰有2人的概率．
参考公式与临界表：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
| P（K2≥k） | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
16．
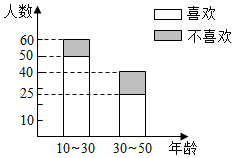某电视台为调查市民对本台某节目的喜爱是否与年龄有关，随机抽取了100名市民，其中是否喜欢该节目的人数如图所示：
（1）写出列表中a，b，c，d的值；
（2）判断是否有99%的把握认为喜欢该节目与年龄有关，说明你的理由；
（3）现计划在这次调查中按年龄段用分层抽样的方法选取5名市民，并从中抽取2名幸运市民，求2名幸运市民中至少有一人在30-50岁之间的概率．
下面的临界值表供参考：
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（a+c）（c+d）（d+b）}$，其中n=a+b+c+d．
某电视台为调查市民对本台某节目的喜爱是否与年龄有关，随机抽取了100名市民，其中是否喜欢该节目的人数如图所示：| 喜欢 | 不喜欢 | 合计 | |
| 10岁至30岁 | a | b | 60 |
| 30岁至50岁 | c | d | 40 |
| 合计 | 75 | 25 | 100 |
（2）判断是否有99%的把握认为喜欢该节目与年龄有关，说明你的理由；
（3）现计划在这次调查中按年龄段用分层抽样的方法选取5名市民，并从中抽取2名幸运市民，求2名幸运市民中至少有一人在30-50岁之间的概率．
下面的临界值表供参考：
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
13．设集合M={x||x-1|≤1}，N={x|y=lg（x2-1）}，则M∩∁RN=（ ）
| A． | [1，2] | B． | [0，1] | C． | （-1，0） | D． | （0，2） |
20．若执行如图的程序框图，输出S的值为-4，则判断框中应填入的条件是（ ）
| A． | k＜14 | B． | k＜15 | C． | k＜16 | D． | k＜17 |