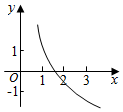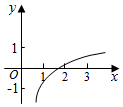题目内容
12.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象过点P($\frac{π}{12}$,0),图象上与点P最近的一个最高点是Q($\frac{π}{3}$,5),则函数f(x)的一个单调递增区间为( )| A. | [-$\frac{π}{3}$,$\frac{π}{3}$] | B. | [-$\frac{π}{4}$,$\frac{π}{2}$] | C. | [-$\frac{π}{3}$,$\frac{π}{6}$] | D. | [0,$\frac{π}{3}$] |
分析 由函数的图象的顶点坐标求出A,由周期求出ω,由特殊点的坐标求出φ的值,可得函数的解析式,由2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$即可解得函数的增区间,比较各个选项即可得解.
解答 解:由题意可得A=5,$\frac{1}{4}•\frac{2π}{ω}$=$\frac{π}{3}$$-\frac{π}{12}$,求得ω=2,
∴y=5sin(2x+φ),
将 ($\frac{π}{3}$,5)代入解析式得:5=5sin($\frac{2π}{3}$+φ),
∴$\frac{2π}{3}$+φ=2kπ+$\frac{π}{2}$,k∈z,
∴φ=-$\frac{π}{6}$+2kπ,k∈Z,
∵|φ|<$\frac{π}{2}$,
令k=0,则有φ=-$\frac{π}{6}$,
∴y=5sin(2x-$\frac{π}{6}$),
∴由2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$(k∈Z),得函数的增区间为[kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$].k∈Z.
∴k=0时,函数的增区间为[$\frac{π}{6}$,$\frac{π}{3}$].比较各个选项可得函数f(x)的一个单调递增区间为[0,$\frac{π}{3}$].
故选:D.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的单调性,属于基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.以椭圆$\frac{x^2}{4}+\frac{y^2}{2}$=1的焦距为实轴,短轴为虚轴的双曲线方程为( )
| A. | x2-4y2=2 | B. | x2-y2=2 | C. | x2-2y2=1 | D. | 2x2-y2=1 |
10.7人站成两排队列,前排3人,后排4人,现将甲、乙、丙三人加入队列,前排加一人,后排加两人,其他人保持相对位置不变,则不同的加入方法种数为( )
| A. | 120 | B. | 240 | C. | 360 | D. | 480 |
7.A,B分别是y=kx和$y=-\frac{1}{k}x$与椭圆$\frac{x^2}{2}+{y^2}=1$的交点,点P在线段AB上,且$\overrightarrow{OA}•\overrightarrow{OP}=\overrightarrow{OB}•\overrightarrow{OP}$,当k变化时,点P一定在( )
| A. | 双曲线x2-2y2=1上 | B. | 椭圆${x^2}+\frac{y^2}{2}=1$上 | ||
| C. | 圆${x^2}+{y^2}=\frac{1}{3}$上 | D. | 圆${x^2}+{y^2}=\frac{2}{3}$上 |
8.已知两条直线a,b和平面α,若a⊥b,b?α,则“a⊥α”是“b∥α”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
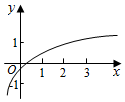
 已知a,b是实数,b>0,函数f(x)=1+asinbx的图象如图所示,则符合条件的函数y=loga(x+b)的图象可能是( )
已知a,b是实数,b>0,函数f(x)=1+asinbx的图象如图所示,则符合条件的函数y=loga(x+b)的图象可能是( )