题目内容
已知函数f(x)=x3-ax(其中a是实数),且f′(1)=3.
(1)求a的值及曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求f(x)在区间[0,2]上的最大值.
(1)求a的值及曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求f(x)在区间[0,2]上的最大值.
考点:利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)求导函数,利用f′(1)=3,确定a的值,从而可得切点坐标,即可求得切线的方程;
(2)求导函数,确定函数的单调性,即可求得函数在区间[0,2]上的最大值.
(2)求导函数,确定函数的单调性,即可求得函数在区间[0,2]上的最大值.
解答:
解:(1)由于函数f(x)=x3-ax,则可得f′(x)=3x2-a,
∵f′(1)=3,∴3-a=3,∴a=0
又当a=0时,f(x)=x3,∴f(1)=1,
所以,曲线y=f(x)在(1,f(1))处的切线方程为y-1=3(x-1),即y=3x-2.
(2)由于f′(x)=3x2≥0,
则f(x)在(0,2)上f′(x)>0,即f(x)在[0,2]上为增函数,
∴f(x)max=f(2)=8.
∵f′(1)=3,∴3-a=3,∴a=0
又当a=0时,f(x)=x3,∴f(1)=1,
所以,曲线y=f(x)在(1,f(1))处的切线方程为y-1=3(x-1),即y=3x-2.
(2)由于f′(x)=3x2≥0,
则f(x)在(0,2)上f′(x)>0,即f(x)在[0,2]上为增函数,
∴f(x)max=f(2)=8.
点评:本题考查导数知识的运用,考查切线方程,考查函数的最值,属于基础题.

练习册系列答案
相关题目
满足条件{a}?A⊆{a,b,c,d}的集合A的个数是( )
| A、5个 | B、6个 | C、7个 | D、8个 |
运行如图的程序,输出的结果为( )


| A、5 | B、9 | C、13 | D、16 |
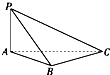 如图所示的三棱锥P-ABC中,底面三角形ABC是边长为2的正三角形且PA=2,PA⊥底面ABC,求此三棱锥外接球的球心到侧面PAB的距离.
如图所示的三棱锥P-ABC中,底面三角形ABC是边长为2的正三角形且PA=2,PA⊥底面ABC,求此三棱锥外接球的球心到侧面PAB的距离.