题目内容
已知椭圆C的中心在坐标原点,短轴长为4,且有一个焦点与抛物线
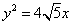 的焦点重合.
的焦点重合.
(1)求椭圆C的方程;
(2)已知经过定点M(2,0)且斜率不为0的直线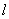 交椭圆C于A、B两点,
交椭圆C于A、B两点,
试问在x轴上是否另存在一个定点P使得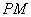 始终平分
始终平分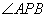 ?若存在,
?若存在,
求出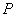 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
【解】:(1)∵椭圆的短轴长为4,∴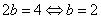 ,
,
又抛物线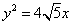 的焦点为
的焦点为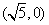 ,∴
,∴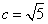 ,
,
则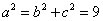 ,∴所求椭圆方程为:
,∴所求椭圆方程为: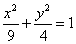 .
.
(2)设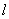 :
: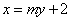 ,代入椭圆方程整理得:
,代入椭圆方程整理得:
则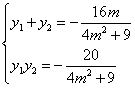 ,假设存在定点
,假设存在定点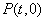 使得
使得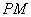 始终平分
始终平分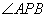 ,
,
则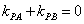
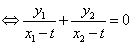

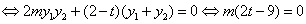 ,∴对于
,∴对于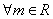 恒成立,∴
恒成立,∴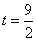 ,故存在定点
,故存在定点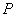 的坐标为
的坐标为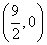 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
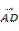 ·
·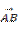 =
= ,则
,则 x3+ax-b在区间[-1,1]上有且仅有一个零点的概率为________.
x3+ax-b在区间[-1,1]上有且仅有一个零点的概率为________. 所在平面内一点,若
所在平面内一点,若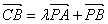 ,其中
,其中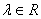 ,则P点一定在( )
,则P点一定在( )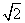 的正方形
的正方形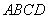 沿对角线
沿对角线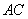 折成一个直二面角
折成一个直二面角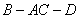 ,则四面体
,则四面体 等于( )
等于( ) (
( 为虚数单位)为纯虚数数,则
为虚数单位)为纯虚数数,则 的为
的为 B.
B. C.
C. D.
D.
 ,则
,则 ”时,下列假设的结论正确的是( )
”时,下列假设的结论正确的是( ) B.
B.
 D.
D.
 的值.
的值.