题目内容
(文)设函数y=xsinx+cosx的图象上的点(x0,y0)处的切线的斜率为k,若k=g(x0),则函数k=g(x0)的图象大致为( )
A、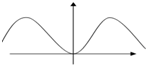 |
B、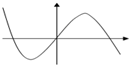 |
C、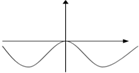 |
D、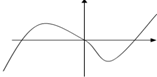 |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:先根据导数的几何意义写出g(x)的表达式.再根据图象的对称性和函数值的分布,逐一判断.
解答:
解:由题意,得g(x)=xcosx,因为g(-x)=-g(x)所以它是奇函数,
k=g(x0)=y′(x0)=x0cosx0,图象关于原点对称,排除A,C,排除B,C.
又当0<x<1<
时,cosx>0,∴xcosx>0,知D项不符合,
故选:B.
k=g(x0)=y′(x0)=x0cosx0,图象关于原点对称,排除A,C,排除B,C.
又当0<x<1<
| π |
| 2 |
故选:B.
点评:对于这样的图象信息题,要根据选项,找出区分度,如图象的对称性,单调性,函数值的特征等,再逐一判断.在选择题的作答中,排除法一直是切实有效的方法之一,特别是这样的图象题,优势尤为明显.

练习册系列答案
相关题目
若不等式|8x+9|<7和不等式ax2+bx-2>0的解集相同,则a、b的值为( )
| A、a=-8 b=-10 |
| B、a=-4 b=-9 |
| C、a=-1 b=9 |
| D、a=-1 b=2 |
已知PA⊥平面ABC,AB=AC,D为BC的中点,则∠PDB( )
| A、等于90° |
| B、小于90° |
| C、大于90° |
| D、无法确定大小 |
在等差数列{an}中,已知a2=2,a4=6,则a6等于( )
| A、6 | B、8 | C、10 | D、12 |
已知正三角形ABC的边长为2a,那么△ABC的直观图△A′B′C′的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个正四面体外切于球O1,同时又内接于球O2,则球O1与球O2的体积之比为( )
A、1:3
| ||
B、1:6
| ||
| C、1:8 | ||
| D、1:27 |
已知函数f(x)=-
,设其在x0处有最大值,则下列说法正确的是( )
| xlnx |
| 1+x |
A、f(x0)>
| ||
B、f(x0)<
| ||
C、f(x0)=
| ||
D、f(x0)与
|
若双曲线的渐近线为y=±
x,且过点M(2,-1),则双曲线的方程为( )
| ||
| 2 |
A、x2-
| ||
B、
| ||
C、
| ||
D、y2-
|