题目内容
根据如图给出的数塔猜测123456×9+8=（ ）
| A、1111110 |
| B、1111111 |
| C、1111112 |
| D、1111113 |
考点：归纳推理
专题：推理和证明
分析：分析已知中的数塔，可知，等式右边各数位上的数字均为1，位数跟等式左边的第二个加数相同，进而得到答案．
解答：
解：由1×9+2=11；
12×9+3=111；
123×9+4=1111；
1234×9+5=11111；
…
归纳可得：等式右边各数位上的数字均为1，位数跟等式左边的第二个加数相同，
∴123456×9+8=123456×9+7+1=11111111+1=1111112，
故选：C
12×9+3=111；
123×9+4=1111；
1234×9+5=11111；
…
归纳可得：等式右边各数位上的数字均为1，位数跟等式左边的第二个加数相同，
∴123456×9+8=123456×9+7+1=11111111+1=1111112，
故选：C
点评：归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．
练习册系列答案
相关题目
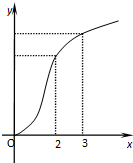已知函数f（x）的图象如图所示，f′（x）是f（x）的导函数，则下列数值排序正确的是（ ）A、0＜f′（2）＜f′（3）＜
| ||
B、0＜f′（3）＜
| ||
C、0＜f′（3）＜f′（2）＜
| ||
D、0＜
|
（文科）已知-3＜a＜-2，3＜b＜4，则
的取值范围为（ ）
| a2 |
| b |
| A、（1，3） | ||||
B、（
| ||||
C、（
| ||||
D、（
|
椭圆
+
=1的焦点坐标是（ ）
| x2 |
| 10 |
| y2 |
| 6 |
| A、（0，-4），（0，4） |
| B、（-4，0），（4，0） |
| C、（-2，0），（2，0） |
| D、（0，-2），（0，2） |
函数f（x）=xsinx的导数是（ ）
| A、xcosx |
| B、sinx |
| C、sinx+xcosx |
| D、sinx-xcosx |
设全集U={1，2，3，4，5，6，7}，集合A={1，3，5}，集合B={2，4，5}，则（∁UA）∩B=（ ）
| A、{1，3，5} |
| B、{1，5} |
| C、{2，4} |
| D、{2，4，6} |