Question

已知x，y满足

5x-3y≤15 y≤x+1 x-2y≤4

，则z=2x+y的最大值是

 

．

Answer 1

考点：简单线性规划

专题：不等式的解法及应用

分析：要先根据约束条件画出可行域，再转化目标函数，把求目标函数的最值问题转化成求截距的最值问题．

解答： 解：由约束条件

5x-3y≤15 y≤x+1 x-2y≤4

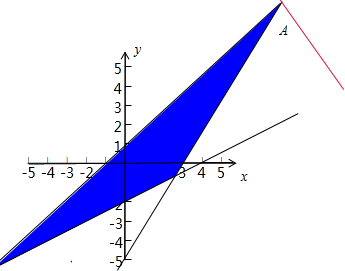
画出可行域如图：
目标函数可化为y=-2x+z，得到一簇斜率为-2，截距为z的平行线
要求z的最大值，须保证截距最大
由图象知，当目标函数的图象过点A是截距最大，由

5x-3y=15 y=x+1

，可得

x=9 y=10

点A的坐标为（9，10）
∴z的最大值为2×9+10=28，
故答案为：28．

点评：本题考查线性规划，须准确画出可行域．还要注意目标函数的图象与可行域边界直线的倾斜程度（斜率的大小）．属中档题．