题目内容
1．圆x2+y2=9，以M（2，1）为中点的弦所在的直线方程为（ ）| A． | x+2y-4=0 | B． | 4x+y-9=0 | C． | 2x-y-3=0 | D． | 2x+y-5=0 |
分析 求出kOM=$\frac{1}{2}$，即可求出以点M（2，1）为中点的弦所在直线方程．
解答 解：x2+y2=9的圆心为（0，0），则kOM=$\frac{1}{2}$，
∴以点M（2，1）为中点的弦所在直线方程为y-1=-2（x-2），即2x+y-5=0．
故选D．
点评 本题考查轨迹方程，求出kOM=$\frac{1}{2}$是关键．
练习册系列答案
相关题目
12．
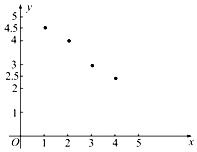如表是某厂1～4月份用水量（单位：百吨）的一组数据．由散点图可知，用水量y与月份x之间有较好的线性相关关系，其线性回归方程是$\stackrel{∧}{y}$=-0.7x+a，则a=（ ）
如表是某厂1～4月份用水量（单位：百吨）的一组数据．由散点图可知，用水量y与月份x之间有较好的线性相关关系，其线性回归方程是$\stackrel{∧}{y}$=-0.7x+a，则a=（ ）| 月份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
| A． | 10.5 | B． | 5.15 | C． | 5.2 | D． | 5.25 |
9．已知在极坐标系中，点A（2，$\frac{π}{2}$），B（$\sqrt{2}$，$\frac{3π}{4}$），O（0，0），则△ABO为（ ）
| A． | 正三角形 | B． | 直角三角形 | C． | 等腰锐角三角形 | D． | 等腰直角三角形 |
16．已知三点A（-1，-1），B（1，x），C（2，5）共线，则x的值是（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
13．集合$A=\left\{{x|f（x）=\sqrt{{2^x}-1}}\right\}$，$B=\left\{{y|y={{log}_2}（{{2^x}+2}）}\right\}$，则A∩∁RB=（ ）
| A． | （1，+∞） | B． | [0，1] | C． | [0，1） | D． | [0，2） |