题目内容
10.某个不透明的盒子里有5枚质地均匀、大小相等的铜币,铜币有两种颜色,一种为黄色,一种为绿色.其中黄色铜币两枚,标号分别为1,2,绿色铜币三枚,标号分别为1,2,3.(1)从该盒子中任取2枚,试列出一次实验所有可能出现的结果;
(2)从该盒子中任取2枚,求这两枚铜币颜色不同且标号之和大于3的概率.
分析 (1)利用列举法能列出一次实验所有可能出现的结果.
(2)从该盒子中任取2枚,列举法这两枚铜币颜色不同且标号之和大于3包含的基本事件,由此能求出这两枚铜币颜色不同且标号之和大于3的概率.
解答 解:(1)一次试验的所有可能结果为:
(黄1,黄2),(黄1,绿1),(黄1,绿2),(黄1,绿3),(黄2,绿1),
(黄2,绿2),(黄2,绿3),(绿1,绿2),(绿1,绿3),(绿2,绿3),
共有10种.
(2)从该盒子中任取2枚,这两枚铜币颜色不同且标号之和大于3包含的基本事件有:
(黄2,绿2),(黄2,绿3),(黄1,绿3),共3种,
∴这两枚铜币颜色不同且标号之和大于3的概率P=$\frac{3}{10}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
1.圆x2+y2=9,以M(2,1)为中点的弦所在的直线方程为( )
| A. | x+2y-4=0 | B. | 4x+y-9=0 | C. | 2x-y-3=0 | D. | 2x+y-5=0 |
18.某质点运动的距离y与时间t的关系为y=t+lnt,那么这个质点在t=1时的瞬时速度为( )
| A. | e | B. | 2 | C. | 1 | D. | $\frac{1}{e}$ |
5.如图所示是一个容量为200的样本的重量频率分布直方图,则由图可估计该样本重量的平均数为( )

| A. | 11 | B. | 11.5 | C. | 12 | D. | 12.5 |
17.若变量x,y满足条$\left\{\begin{array}{l}y≥0\\ x+2y≥1\\ x+4y≤3\end{array}\right.$,则z=(x+1)2+y2的最小值是( )
| A. | 1 | B. | 2 | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{4}{5}$ |
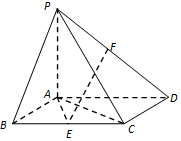 如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,PA=AB.
如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,PA=AB.