题目内容

在等差数列{an}中，a1=-2013，其前n项和为Sn，若
S12
12
-
S10
10
=2，则S2014的值等于
 
．
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：设等差数列的公差为d，利用等差数列的求和公式及
S12
12
-
S10
10
=2可求得公差d，再用求和公式可得答案．
解答： 解：设等差数列的公差为d，
∵
S12
12
-
S10
10
=2，
∴a12-a10=4，
∴2d=4，得d=2，
∴S2014=2014×（-2013）+
2014×2013
2
×2=0，
故答案为：0．
点评：此题考查了等差数列的前n项和公式，以及等差数列的性质，其中求出公差d的值，是解题的关键．
练习册系列答案
相关题目
“a=b”是“
a
=
b
”的
 
条件．（从“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”中选择一个填空）．
不等式
2-x
x+1
≥0的解集为
 
．
过点P（2，4）作圆（x-1）2+（y+3）2=1的切线，则切线方程为
 
．
在等比数列{an}中：若Sn为{an}的前n项和，S4=2，S8=6，则a17+a18+a19+a20=
 
．
设f（x）是定义在R上以3为周期的奇函数，且f（-1）=1，若cosα=-
70
10
，则f（12）+f（10cos2α）=
 
．
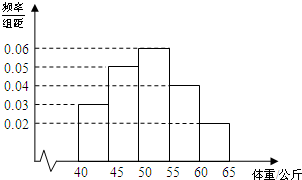某校高三年级共1200人．学校为了检查同学们的健康状况，随机抽取了高三年级的100名同学作为样本，测量他们的体重（单位：公斤），体重的分组区间为[40，45），[45，50），[50，55），（55，60），[60，65]，由此得到样本的频率分布直方图，如图．根据频率分布直方图，估计该校高三年级体重低于50公斤的人数为
 
．
椭圆2x2+3y2=12的两焦点之间的距离为
 
．
已知点A（2，5）、B（4，1），直线l过点（-1，-3）且与线段AB有交点，则直线l的斜率k的取值范围为（　　）
A、（
4
5
，
8
3
）
B、[
4
5
，
8
3
]
C、（-∞，
4
5
）∪（
8
3
，+∞）
D、（-∞，
4
5
）∪[
8
3
，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网