题目内容
函数y=f(x)的图象在点P(3,f(3))处的切线方程为y=x+2,f′(x)为f(x)的导函数,则f(3)+f′(3) .
考点:导数的运算
专题:导数的综合应用
分析:根据导数的几何意义,即可得到结论.
解答:
解:∵函数y=f(x)的图象在点P(3,f(3))处的切线方程为y=x+2,
∴f(3)=3+2=5,f'(3)=1,
即f(3)+f′(3)=5+1=6,
故答案为:6.
∴f(3)=3+2=5,f'(3)=1,
即f(3)+f′(3)=5+1=6,
故答案为:6.
点评:本题主要考查导数的基本运算,根据导数的几何意义是解决本题的关键,比较基础.

练习册系列答案
相关题目
下列说法中错误的是( )
| A、对于命题p:x0∈R,sin x0>1,则¬p:x∈R,sin x≤1 |
| B、命题“若0<a<1,则函数f(x)=ax在R上是增函数”的逆命题为假命题 |
| C、若p∨q为真命题,则p,q均为真命题 |
| D、命题“若x2-x-2=0,则x=2”的逆否命题是“若x≠2,则x2-x-2≠0” |
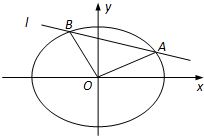 在平面直角坐标系xOy中,设椭圆C的中心在原点,焦点在x轴上,短半轴长为2,椭圆C长轴的右端点到其右焦点的距离为
在平面直角坐标系xOy中,设椭圆C的中心在原点,焦点在x轴上,短半轴长为2,椭圆C长轴的右端点到其右焦点的距离为 如图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图.从这个茎叶图可以看出甲、乙两名运动员得分的中位数分别是
如图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图.从这个茎叶图可以看出甲、乙两名运动员得分的中位数分别是