题目内容
在等差数列{an}中,a9=
a12+6,则数列{an}的前11项和S11等于 .
| 1 |
| 2 |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由已知条件,利用等差数列的通项公式推导出a1+5d=12,由此利用等差数列的前n项和公式能求出S11.
解答:
解:∵等差数列{an}中,a9=
a12+6,即2a9=a12+12,
∴2(a1+8d)=a1+11d+12,
∴a1+5d=12,
∴S11=
(a1+a11)
=
(2a1+10d)
=11(a1+5d)
=11×12
=132.
故答案为:132.
| 1 |
| 2 |
∴2(a1+8d)=a1+11d+12,
∴a1+5d=12,
∴S11=
| 11 |
| 2 |
=
| 11 |
| 2 |
=11(a1+5d)
=11×12
=132.
故答案为:132.
点评:本题考查数列的前11项和的求法,是基础题,解题时要熟练掌握等差数列的通项公式和前n项和公式.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
已知|
|=4,
为单位向量,当
,
的夹角为
时,
+
在
-
上的投影为( )
| a |
| e |
| a |
| e |
| 2π |
| 3 |
| a |
| e |
| a |
| e |
| A、5 | ||||
B、
| ||||
C、
| ||||
D、
|
下列说法不正确的是( )
| A、所有的对立事件都是互斥事件 | ||
B、先后抛掷两枚大小一样的硬币,两枚都出现反面的概率是
| ||
| C、事件“直线y=k(x+1)过点(-1,0)”是必然事件 | ||
D、某红绿灯路口,红灯时间为30秒,黄灯时间为5秒,绿灯时间为45秒,当你到这个路口时,看到黄灯的概率是
|
下列命题中的假命题是( )
| A、?x∈R,2x-1>0 |
| B、?x∈R,lgx<1 |
| C、?x∈N+,(x-1)2>0 |
| D、?x∈R,tanx=2 |
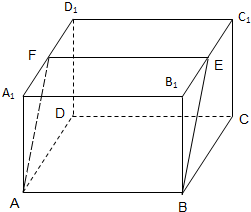 如图,直四棱柱ABCD-A1B1C1D1的底面边长为2的菱形,∠BAD=60°,高为1,过底边AB作一截面ABEF,若BE=2
如图,直四棱柱ABCD-A1B1C1D1的底面边长为2的菱形,∠BAD=60°,高为1,过底边AB作一截面ABEF,若BE=2 如图,矩形ABEF和正方形ABCD有公共边AB,它们所在平面成60°的二面角,AB=CB=2a,BE=a,则DE=
如图,矩形ABEF和正方形ABCD有公共边AB,它们所在平面成60°的二面角,AB=CB=2a,BE=a,则DE=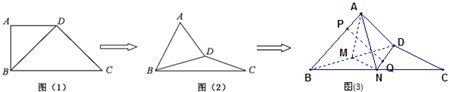 在直角梯形ABCD中,AD∥BC,
在直角梯形ABCD中,AD∥BC,