题目内容
7.已知双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别是F1、F2,其一条渐近线方程为$y=\sqrt{2}x$,点P($\sqrt{3}$,y0)在双曲线上.则$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=-1.分析 求得双曲线的渐近线方程,可得b=2,求得c,将P的坐标代入双曲线的方程,可得y02=2,由向量的数量积的坐标表示计算即可得到所求值.
解答 解:双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{{b}^{2}}$=1的渐近线方程为y=±$\frac{b}{\sqrt{2}}$x,
由题意可得$\frac{b}{\sqrt{2}}$=$\sqrt{2}$,解得b=2,
又c=$\sqrt{2+4}$=$\sqrt{6}$,
点P($\sqrt{3}$,y0)在双曲线上,可得$\frac{3}{2}$-$\frac{{{y}_{0}}^{2}}{4}$=1,
即有y02=2,
则$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=(-$\sqrt{6}$-$\sqrt{3}$,-y0)•($\sqrt{6}$-$\sqrt{3}$,-y0)
=(-$\sqrt{6}$-$\sqrt{3}$)($\sqrt{6}$-$\sqrt{3}$)+y02=3-6+2=-1.
故答案为:-1.
点评 本题考查向量的数量积的坐标表示,考查双曲线的渐近线方程的运用,以及点满足双曲线的方程,考查化简整理的运算能力,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
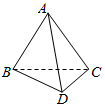
18.如图,空间四边形ABCD中,“AC=AD”“BC=BD”则AB与CD所成的角为( )

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
17.tan70°cos10°+$\sqrt{3}$sin10°tan70°-2sin50°=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
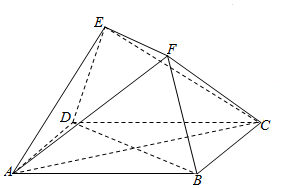 如图,多面体ABCDEF中,四边形ABCD是边长为2的正方形,四边形EFBD为等腰梯形,EF∥BD,EF=$\frac{1}{2}$BD,平面EFBD⊥平面ABCD.
如图,多面体ABCDEF中,四边形ABCD是边长为2的正方形,四边形EFBD为等腰梯形,EF∥BD,EF=$\frac{1}{2}$BD,平面EFBD⊥平面ABCD.