题目内容

18．如图，空间四边形ABCD中，“AC=AD”“BC=BD”则AB与CD所成的角为（　　）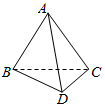
A．30°B．45°C．60°D．90°

分析 取CD中点O，连结BO、AO，推导出CD⊥平面AOB，从而得到AB与CD所成的角为90°．

解答 解：空间四边形ABCD中，
取CD中点O，连结BO、AO，
∵AC=AD，BC=BD，
∴BO⊥CD，AO⊥CD，
∵BO∩AO=O，
∴CD⊥平面AOB，
∵AB?平面AOB，∴CD⊥AB，
∴AB与CD所成的角为90°．
故选：D．

点评 本题考查异面直线所成角的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．

练习册系列答案
相关题目
5．设f（x）（x∈R）是以2为周期的奇函数，当x∈（0，1）时，f（x）=2x，则f（${log}_{\frac{1}{2}}$23）的值是-$\frac{23}{16}$．
6．已知直线l经过点A（2，1），B（m2+1，2），
（1）求直线l的方程；
（2）求直线l的倾斜角的取值范围．
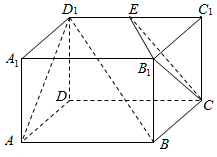6．已知长方体AC1中，AD=AB=2，AA1=1，E为D1C1的中点，如图所示．
（Ⅰ）在所给图中画出平面ABD1与平面B1EC的交线（不必说明理由）；
（Ⅱ）证明：BD1∥平面B1EC；
（Ⅲ）求平面ABD1与平面B1EC所成锐二面角的大小．
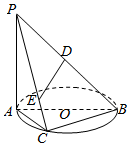13．如图，AB是圆O的直径，点C是半圆的中点，PA⊥平面ABC，PA=AB，PB=6D是PB的中点，E是PC上一点．
（Ⅰ） 若DE⊥PB，求$\frac{PE}{EC}$的值；
（Ⅱ）若点Q是平面ABC内一点，且|QA|=2|QC|，求点Q在△ABC内的轨迹长度．
3．已知正三棱柱ABC-A1B1C1的各棱长都为1，M是底面BC边上的中点，N是侧棱CC1上的点，且$CN=\frac{1}{4}C{C_1}$，则AB1与MN所成的角是$\frac{π}{2}$．
10．如图1，在Rt△ABC中，∠ACB=30°，∠ABC=90°，D为AC中点，AE⊥BD于E，延长AE交BC与F，将△ABD沿BD折起，使平面ABD⊥平面BCD，如图2所示
（Ⅰ） 求证：平面AEF⊥平面BCD；
（Ⅱ） 在线段AF上是否存在点M使得EM∥平面ADC？若存在，请指明点M的位置；若不存在，请说明理由．
7．已知双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别是F1、F2，其一条渐近线方程为$y=\sqrt{2}x$，点P（$\sqrt{3}$，y0）在双曲线上．则$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=-1．
8．已知函数$f（x）=\left\{\begin{array}{l}{{2}^{x-1}-2，x≤1}\\{-lo{g}_{2}（x+1），x＞1}\end{array}\right.$且f（a）≥-2，则实数a的取值范围是（　　）
A．（-∞，1]B．[3，+∞）C．（-∞，3]D．[1，3]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网