题目内容

已知log
x
(2X)=
1
2
，求x．
考点：对数的运算性质
专题：函数的性质及应用
分析：把对数式log
x
(2x)=
1
2
，化为指数式(
x
)
1
2
=2x，因此x=16x4，由于x＞0且x≠1，可得16x3=1，即可得出．
解答： 解：∵log
x
(2x)=
1
2
，
∴(
x
)
1
2
=2x，
∴x=（2x）4=16x4，
∵x＞0且x≠1，
∴16x3=1，
∴x=
3
1
16
=
34
4
．
点评：本题考查了对数式化为指数式及其运算性质，属于基础题．
练习册系列答案
相关题目
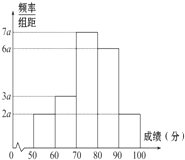从100名学生中抽取20名学生某次数学考试成绩（单位：分）的频率分布直方图如下：
（1）求频率分布直方图中a的值；
（2）估计总体中成绩落在[50，70）中的学生人数；
（3）估计总体的中位数．
已知定义在[-1，1]上的函数f（x）=x2+x2014+1，则不等式f（x-1）＞f（2x）的解集为
 
．
函数f（x）=sin（ωx+φ）（A＞0，ω＞0，-π＜φ＜0），y=f（x）的周期为π，其图象最高点（
5π
8
，1）．
（1）求该函数的解析式；
（2）用“五点法”画出函数y=f（x）在区间[0，π]上的图象；
（3）方程f（x）=a在[
3π
8
，
7π
8
]上有两个相异的根x1、x2，求x1+x2的值．
已知数列{an}是等差数列，a1＞0，其前n项和Sn满足S14＜S7＜S13，则当n=
 
时，Sn最大．
命题p：x＞1，命题q：
x-1
x
＞0，则p是 q成立的
 
条件．
已知集合A={x|（a-2）x2+2x+1=0}只有一个元素
（1）求实数a的值；
（2）若f（x）=xa+x-a在区间[-2，-1]上是减函数，解不等式：f（-bx）＜f（-bx+1）（b＞0，b≠1）
设函数f（x）=msinx+cosx（x∈R）的图象经过点（
π
2
，1）．
（1）求y=f（x）的解析式；
（2）求函数的最小正周期和最大值和单调递增区间．
若ac＞0且bc＜0，直线ax+by+c=0不通过第
 
象限．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网