题目内容
已知椭圆C的中心在原点,焦点在x轴上,且过点A(1,
)和B(-
,-
).
(1)求椭圆C的方程;
(2)若椭圆E与椭圆C有相同的焦点,且过点P(2,-
),求椭圆E的方程.
| 3 |
| 2 |
| 2 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)若椭圆E与椭圆C有相同的焦点,且过点P(2,-
| ||
| 2 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)设椭圆的方程为
+
=1(a>b>0),代入点A(1,
)和B(-
,-
),求出a,b,即可求椭圆C的方程;
(2)设椭圆方程为
+
=1(m>0),代入点P(2,-
),求出m,即可求椭圆E的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 2 |
| ||
| 2 |
(2)设椭圆方程为
| x2 |
| m |
| y2 |
| m-1 |
| ||
| 2 |
解答:
解:(1)设椭圆的方程为
+
=1(a>b>0),则
∵过点A(1,
)和B(-
,-
),
∴
,
∴a=2,b=
,
∴椭圆C的方程为
+
=1;
(2)设椭圆方程为
+
=1(m>0),
∵椭圆过点P(2,-
),
∴
+
=1,
∴m=8,
∴椭圆方程为
+
=1.
| x2 |
| a2 |
| y2 |
| b2 |
∵过点A(1,
| 3 |
| 2 |
| 2 |
| ||
| 2 |
∴
|
∴a=2,b=
| 3 |
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设椭圆方程为
| x2 |
| m |
| y2 |
| m-1 |
∵椭圆过点P(2,-
| ||
| 2 |
∴
| 4 |
| m |
| ||
| m-1 |
∴m=8,
∴椭圆方程为
| x2 |
| 8 |
| y2 |
| 7 |
点评:本题考查椭圆方程,考查学生的计算能力,正确设椭圆方程是关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
下列各组两个集合M和N,表示同一集合的是( )
| A、M={π},N={3.14159} |
| B、M={2,3},N={(2,3)} |
| C、M={(x,y)|x+y=1},N={y|x+y=1} |
| D、M={x|x2+1=0},N=∅ |
已知f(x)=
sin2x-cos2x,则将f(x)的图象向右平移
个单位所得曲线的一个对称中心为( )
| 3 |
| π |
| 3 |
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|
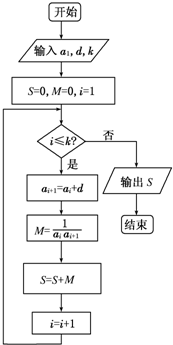 已知等差数列{an}的各项均为正数,观察如图所示的程序框图,当k=5,k=10时,分别有S=
已知等差数列{an}的各项均为正数,观察如图所示的程序框图,当k=5,k=10时,分别有S=| 5 |
| 11 |
| 10 |
| 21 |
| A、an=2n+1 |
| B、an=2n+3 |
| C、an=2n-1 |
| D、an=2n-3 |