题目内容
4.二手车经销商小王对其所经营的某一型号二手汽车的使用年数x(0<x≤10)与销售价格y(单位:万元/辆)进行整理,得到如下的对应数据:| 使用年数 | 2 | 4 | 6 | 8 | 10 |
| 售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(2)已知小王只收购使用年限不超过10年的二手车,且每辆该型号汽车的收购价格为ω=0.03x2-1.81x+16.2万元,根据(1)中所求的回归方程,预测x为何值时,小王销售一辆该型号汽车所获得的利润L(x)最大?
(销售一辆该型号汽车的利润=销售价格-收购价格)
参考公式:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
分析 (1)计算平均数,分别求出$\widehat{b}$,$\widehat{a}$的值,求出回归方程即可;
(2)求出方程L(x),根据二次函数的性质求出函数的最大值即可.
解答 解:(1)由已知:$\overline x=6$,$\overline y=10$,…(2分)
$\sum_{i=1}^5{x_i}{y_i}=242$,$\sum_{i=1}^5{{x_i}^2}=220$$\hat b=\frac{{\sum_{i=1}^5{x_i}{y_i}-5\overline x\overline y}}{{\sum_{i=1}^5{{x_i}^2}-5{{\overline x}^2}}}=-1.45$,…(5分)
$\hat a=\overline y-\hat b\overline x=18.7$…(6分)
所求线性回归直线方程为$\hat y=-1.45x+18.7$…(7分)
(2)L(x)=y-ω=-1.45x+18.7-(0.03x2-1.81x+16.2)
=-0.03x2+0.36x+2.5=-0.03(x-6)2+3.58(0<x≤10)…(10分)
∵0<x≤10
∴当x=6时,L(x)max=3.58(万元) …(11分)
所以预测x=6时,销售一辆该型号汽车所获得的利润L(x)最大.…(12分)
点评 本题考查了求回归方程问题,考查二次函数的性质以及求函数最值问题,是一道中档题.

练习册系列答案
相关题目
12.两个实习生每人加工一个零件,加工为一等品的概率分别为$\frac{2}{3}$和$\frac{1}{2}$,两个零件是否加工为一等品相互独立,则这两个零件中至少有一个加工为一等品的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
9.袋中装有红球3个、白球2个、黑球1个,从中任取2个,则互斥而不对立的两个事件是( )
| A. | 至少有一个白球;至少有一个红球 | B. | 至少有一个白球;红、黑球各一个 | ||
| C. | 恰有一个白球;一个白球一个黑球 | D. | 至少有一个白球;都是白球 |
14.在区间[-1,1]上随机取一个数x,x2的值介于0到$\frac{1}{4}$之间的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
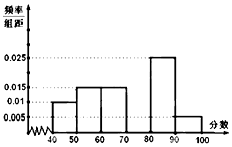 某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题: