题目内容

6．已知条件p：log2（x-1）＜1的解，q：x2-2x-3＜0的解，则p是q的（　　）条件．
A．充分非必要B．必要非充分
C．充分必要D．既非充分又非必要

分析 求出p，q的等价条件，利用充分条件和必要条件的定义进行判断即可．

解答 解：由log2（x-1）＜1，
得：0＜x-1＜2，即1＜x＜3，
即p：1＜x＜3，
由x2-2x-3＜0得-1＜x＜3，
即q：-1＜x＜3，
∴p是q的充分不必要条件，
故选：A．

点评 本题主要考查充分条件和必要条件的判断，利用不等式的解法求出不等式的等价条件是解决本题的关键，比较基础．

练习册系列答案
相关题目
6．在直角坐标系xOy中，曲线C1的参数方程为$\left\{\begin{array}{l}x=1+acost\\ y=asint\end{array}$（t为参数，a＞0），在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=2sinθ．
（1）求曲线C1的普通方程，并将C1的方程化为极坐标方程；
（2）直线C3的极坐标方程为θ=$\frac{π}{4}$，若曲线C1与C2的公共点都在C3上，求a的值．
7．已知函数$f（x）=x-mlnx-\frac{m-1}{x}（{m∈R}）$，$g（x）=\frac{1}{2}{x^2}+{e^x}-x{e^x}$，
（1）当x∈[1，e]，求f（x）的最小值，
（2）当m≤2时，若存在${x_1}∈[{e，{e^2}}]$，使得对任意x2∈[-2，0]，f（x1）≤g（x2）成立，求实数m的取值范围．
4．已知幂函数y=xa的图象过点（2，8），则这个函数的解析式是y=x3．
1．已知函数f（x）=2sin2x+cos（2x-$\frac{π}{3}$）-1
（1）求函数f（x）的最小正周期；
（2）求函数f（x）在区间[$\frac{π}{12}$，$\frac{π}{2}$]上的值域．
11．已知个面向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1，|$\overrightarrow{a}$-2$\overrightarrow{b}$|=$\sqrt{21}$，且$\overrightarrow{a}$与$\overrightarrow{b}$夹角为120°，则|$\overrightarrow{b}$|=2．
18．已知命题p：“?x∈R时，都有${x^2}-x+\frac{1}{4}＞0$”； 命题q：“?x°∈R，使sinx°+cosx°=2时”，则下列判断正确的是（　　）
A．p∨q为假命题B．p∧q为真命题C．￢p∧q为真命题D．￢p∨￢q为假命题
15．茎叶图如图1，为高三某班60名学生的化学考试成绩，算法框图如图2中输入的a1为茎叶图中的学生成绩，则输出的m，n分别是（　　）
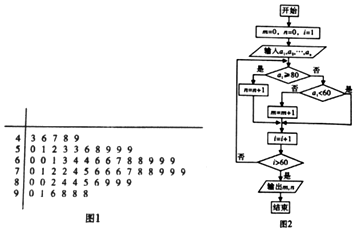
A．m=29，n=15B．m=29，n=16C．m=15，n=16D．m=16，n=15
16．设双曲线C的焦点在x轴上，渐近线方程为$y=±\frac{{\sqrt{2}}}{2}x$，则其离心率为$\frac{\sqrt{6}}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网