题目内容
为得到函数y=cos(2x+
)的图象,只需将函数y=sin2x的图象( )
| 2π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:将函数f(x)=sin2x转化为f(x)=cos(2x-
),利用函数y=Asin(ωx+φ)的图象变换即可求得答案.
| π |
| 2 |
解答:
解:∵y=f(x)=sin2x=cos(2x-
),
∴f(x+
)=cos[2(x+
)-
]=cos(2x+
),
∴为了得到y=cos(2x+
)的图象,只需将函数y=sin2x的图象向左平移
个长度单位,
故选:A.
| π |
| 2 |
∴f(x+
| 7π |
| 12 |
| 7π |
| 12 |
| π |
| 2 |
| 2π |
| 3 |
∴为了得到y=cos(2x+
| 2π |
| 3 |
| 7π |
| 12 |
故选:A.
点评:本题考查诱导公式与函数y=Asin(ωx+φ)的图象变换,考查转化思想与运算能力,属于中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
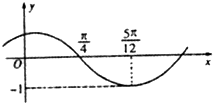 从函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
从函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<| π |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
若复数(x2-1)+(x-1)i对应的点在虚轴上,则实数x的值为( )
| A、-1或1 | B、0 | C、1 | D、-1 |
等比数列{an}满足a2+a4=20,a3+a5=40,则公比q=( )
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
在△ABC中,|AB|=3,|AC|=2,
=
+
,则直线AD通过△ABC的( )
| AD |
| 1 |
| 2 |
| AB |
| 3 |
| 4 |
| AC |
| A、垂心 | B、外心 | C、重心 | D、内心 |
3位数学家,4位物理学家,站成两排照像.其中前排3人后排4人,要求数学家要相邻,则不同的排队方法共有( )
| A、5040种 | B、840种 |
| C、720种 | D、432种 |