题目内容
已知m,n是不重合的直线,α,β是不重合的平面,给出下列命题:
①若m⊥α,m?β,则α⊥β;
②若m?α,n?α,m∥β,n∥β,则α∥β;
③如果m?α,n?α,m,n是异面直线,则n与α相交;
④若α∩β=m,n∥m,且n?β,则n∥α,且n∥β.
其中正确命题的个数是( )
①若m⊥α,m?β,则α⊥β;
②若m?α,n?α,m∥β,n∥β,则α∥β;
③如果m?α,n?α,m,n是异面直线,则n与α相交;
④若α∩β=m,n∥m,且n?β,则n∥α,且n∥β.
其中正确命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:①根据面面垂直的判定定理即可判断出;
②若m?α,n?α,m∥β,n∥β,只有当m,n是相交直线时,才能得出α∥β;
③如果m?α,n?α,m,n是异面直线,则n与α相交或n∥α,即可判断出;
④根据线面平行的判定与性质定理即可判得出.
②若m?α,n?α,m∥β,n∥β,只有当m,n是相交直线时,才能得出α∥β;
③如果m?α,n?α,m,n是异面直线,则n与α相交或n∥α,即可判断出;
④根据线面平行的判定与性质定理即可判得出.
解答:
解:已知m,n是不重合的直线,α,β是不重合的平面.
①根据面面垂直的判定定理可得:若m⊥α,m?β,则α⊥β,因此正确;
②若m?α,n?α,m∥β,n∥β,只有当m,n是相交直线时,才能得出α∥β,因此不正确;
③如果m?α,n?α,m,n是异面直线,则n与α相交或n∥α,因此不正确;
④根据线面平行的判定与性质定理可得:若α∩β=m,n∥m,且n?β,则n∥α,且n∥β,或n?α,因此不正确.
综上可得:只有①正确.
故选:A.
①根据面面垂直的判定定理可得:若m⊥α,m?β,则α⊥β,因此正确;
②若m?α,n?α,m∥β,n∥β,只有当m,n是相交直线时,才能得出α∥β,因此不正确;
③如果m?α,n?α,m,n是异面直线,则n与α相交或n∥α,因此不正确;
④根据线面平行的判定与性质定理可得:若α∩β=m,n∥m,且n?β,则n∥α,且n∥β,或n?α,因此不正确.
综上可得:只有①正确.
故选:A.
点评:本题综合考查了线面平行于垂直的位置关系,属于基础题.

练习册系列答案
相关题目
已知a、b都是实数,a≠0,f(x)=|x-1|+|x-2|.
(1)若f(x)>2,求实数x的取值范围;
(2)若|a+b|+|a-b|≥|a|f(x)对满足条件的所有a、b都成立,求实数x的取值范围.
(1)若f(x)>2,求实数x的取值范围;
(2)若|a+b|+|a-b|≥|a|f(x)对满足条件的所有a、b都成立,求实数x的取值范围.
已知a>1,b>1,且lnalnb=
,则ab( )
| 1 |
| 4 |
| A、有最大值1 |
| B、有最小值1 |
| C、有最大值e |
| D、有最小值e |
二项式(
-
)n的展开式中第4项为常数项,则常数项为( )
| x |
| 1 | |||
|
| A、10 | B、-10 |
| C、20 | D、-20 |
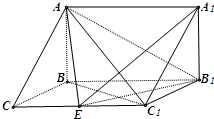 如图,在三棱柱ABC-A1B1C1中,已知BC=1,BB1=2,∠BCC1=90°,AB⊥侧面BB1C1C.
如图,在三棱柱ABC-A1B1C1中,已知BC=1,BB1=2,∠BCC1=90°,AB⊥侧面BB1C1C.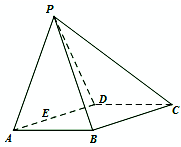 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为等边三角形,平面PAD⊥平面ABCD,且∠DAB=60°,AB=2,E为AD的中点.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为等边三角形,平面PAD⊥平面ABCD,且∠DAB=60°,AB=2,E为AD的中点.