题目内容
20.某程序框图如图所示,若该程序运行后输出的值是$\frac{23}{12}$,则a的值为( )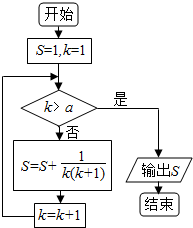
| A. | 13 | B. | 12 | C. | 11 | D. | 10 |
分析 模拟执行程序框图,依次写出每次循环得到的S,k的值,当S=$\frac{23}{12}$时,根据题意,求得此时k的值,应该满足条件k>a,退出循环,输出S的值,从而得解.
解答 解:模拟执行程序框图,可得
S=1,k=1
不满足条件k>a,S=1+$\frac{1}{2}$=2$-\frac{1}{2}$,k=2
不满足条件k>a,S=1+$\frac{1}{2}$+$\frac{1}{2×3}$=2$-\frac{1}{3}$,k=3
不满足条件k>a,S=1+$\frac{1}{2}$$+\frac{1}{2×3}$+$\frac{1}{3×4}$=2$-\frac{1}{4}$,k=4
不满足条件k>a,S=1+$\frac{1}{2}$$+\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$=2-$\frac{1}{5}$,k=5
不满足条件k>a,S=1+$\frac{1}{2}$$+\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$+$\frac{1}{5×6}$=2$-\frac{1}{6}$,k=6
不满足条件k>a,S=1+$\frac{1}{2}$$+\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$+$\frac{1}{5×6}$+$\frac{1}{6×7}$=2-$\frac{1}{7}$,k=7
…
最后一次循环,不满足条件k>a,S=2-$\frac{1}{x}$=$\frac{23}{12}$,k=x+1
满足条件k>a,退出循环,输出S的值为$\frac{23}{12}$.
可解得:x=12,即由题意可得a的值为11.
故选:C.
点评 本题主要考查了循环结构,根据S的值正确判断退出循环的条件是解题的关键,属于基础题.


| A. | 7 | B. | 9 | C. | 11 | D. | 16 |
| A. | 已知直线l,点A∈l,直线m?α,A∉m,则l与m异面 | |
| B. | 已知直线m?α,直线l∥m,则l∥α | |
| C. | 已知平面α、β,直线n⊥α,直线n⊥β,则α∥β | |
| D. | 若直线a、b与α所成的角相等,则a∥b |
| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
| A. | 1+π | B. | 2 | C. | 2+π | D. | π |
| A. | f($-\frac{π}{2}$)<f($\sqrt{2}$)<f(e) | B. | f(e)<f($-\frac{π}{2}$)<f($\sqrt{2}$) | C. | f(e)<f($\sqrt{2}$)<f($-\frac{π}{2}$) | D. | f($\sqrt{2}$)<f($-\frac{π}{2}$)<f(e) |