题目内容
10.已知定义在R上的函数f(x)满足:对任意x1,x2∈R(x1≠x2),均有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0,e为自然对数的底,则( )| A. | f($-\frac{π}{2}$)<f($\sqrt{2}$)<f(e) | B. | f(e)<f($-\frac{π}{2}$)<f($\sqrt{2}$) | C. | f(e)<f($\sqrt{2}$)<f($-\frac{π}{2}$) | D. | f($\sqrt{2}$)<f($-\frac{π}{2}$)<f(e) |
分析 根据条件及增函数的定义容易判断出f(x)在R上单调递增,从而比较$-\frac{π}{2},\sqrt{2},e$这三个数的大小便可得出对应的函数值的大小,从而找出正确选项.
解答 解:∵$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}>0$;
∴对任意的x1,x2∈R,x1<x2时,会得到f(x1)<f(x2);
∴f(x)在R上为增函数;
又$-\frac{π}{2}<\sqrt{2}<e$;
∴$f(-\frac{π}{2})<f(\sqrt{2})<f(e)$.
故选:A.
点评 考查增函数的定义,根据增函数的定义比较函数值大小的方法,清楚$-\frac{π}{2},\sqrt{2},e$这三个数的大小关系.

练习册系列答案
相关题目
20.某程序框图如图所示,若该程序运行后输出的值是$\frac{23}{12}$,则a的值为( )
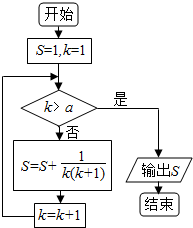

| A. | 13 | B. | 12 | C. | 11 | D. | 10 |
1.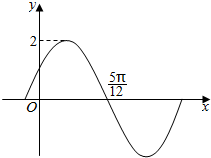 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,且f(0)=f($\frac{π}{3}$),则( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,且f(0)=f($\frac{π}{3}$),则( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,且f(0)=f($\frac{π}{3}$),则( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,且f(0)=f($\frac{π}{3}$),则( )| A. | f(x)的最小正周期为2π | B. | f(x)的图象关于直线x=$\frac{5π}{6}$对称 | ||
| C. | f($\frac{2π}{3}$)=-2 | D. | f(x)在[0,$\frac{π}{4}$]上是增函数 |
5.下列函数中,值域为[1,+∞)的是( )
| A. | y=2x+1 | B. | y=$\sqrt{x-1}$ | C. | y=$\frac{1}{|x|}$+1 | D. | y=x+$\sqrt{x-1}$ |
2.已知log0.3(m+1)<log0.3(2m-1),则m的取值范围是( )
| A. | (-∞,2) | B. | $({\frac{1}{2},2})$ | C. | (2,+∞) | D. | (-1,2) |
19.现用系统抽样方法从已编号(1-60)的60枚新型导弹中,随机抽取6枚进行试验,则所选取的6枚导弹的编号可能是( )
| A. | 5,10,15,20,25,30 | B. | 2,4,8,16,32,48 | ||
| C. | 5,15,25,35,45,55 | D. | 1,12,34,47,51,60 |
 如图所示的四面体OABC中,OA=OB=OC=a,∠AOB=90°,∠BOC=∠AOC=60°,点M,N分别是AB,OC的中点,点S是MN上靠近点N的三等分点.
如图所示的四面体OABC中,OA=OB=OC=a,∠AOB=90°,∠BOC=∠AOC=60°,点M,N分别是AB,OC的中点,点S是MN上靠近点N的三等分点.