题目内容
9.设集合A={(x,y)|x2+y2≤|x|+|y|,x,y∈R},则集合A所表示图形的面积为( )| A. | 1+π | B. | 2 | C. | 2+π | D. | π |
分析 根据不等式,分别讨论x,y的取值,转化为二元二次不等式组,结合圆的性质进行求解即可.
解答 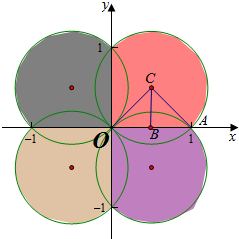 解:若x≥0,y≥0,则不等式等价为x2+y2≤x+y,即(x-$\frac{1}{2}$)x2+(y-$\frac{1}{2}$)2≤$\frac{1}{2}$,
解:若x≥0,y≥0,则不等式等价为x2+y2≤x+y,即(x-$\frac{1}{2}$)x2+(y-$\frac{1}{2}$)2≤$\frac{1}{2}$,
若x≥0,y<0,则不等式等价为x2+y2≤x-y,即(x-$\frac{1}{2}$)x2+(y+$\frac{1}{2}$)2≤$\frac{1}{2}$,
若x≤0,y≤0,则不等式等价为x2+y2≤-x-y,即(x+$\frac{1}{2}$)x2+(y+$\frac{1}{2}$)2≤$\frac{1}{2}$,
若x<0,y≥0,则不等式等价为x2+y2≤-x+y,即(x+$\frac{1}{2}$)x2+(y-$\frac{1}{2}$)2≤$\frac{1}{2}$,
则对应的区域如图:
在第一象限内圆心坐标为C($\frac{1}{2}$,$\frac{1}{2}$),半径=$\frac{\sqrt{2}}{2}$,
则三角形OAC的面积S=$\frac{1}{2}×\frac{\sqrt{2}}{2}×\frac{\sqrt{2}}{2}$=$\frac{1}{4}$,
$\frac{1}{4}$圆的面积为$\frac{1}{4}$×$π×(\frac{\sqrt{2}}{2})^{2}$=$\frac{1•}{8}$π,
则一个弓弧的面积S=$\frac{1•}{8}$π-$\frac{1}{4}$,
则在第一象限的面积S=π×($\frac{\sqrt{2}}{2}$)2-2×($\frac{1•}{8}$π-$\frac{1}{4}$)=$\frac{π}{2}$-$\frac{π}{4}$+$\frac{1}{2}$=$\frac{π}{4}$+$\frac{1}{2}$,
则整个区域的面积S=4×($\frac{π}{4}$+$\frac{1}{2}$)=2+π,
故选:C
点评 本题主要考查区域面积的计算,根据条件利用分类讨论的数学数学化简条件,利用圆的面积公式是解决本题的关键.综合性较强,比较复杂.

 阅读快车系列答案
阅读快车系列答案| A. | 2或5 | B. | -4或2 | C. | 2 | D. | 5 |
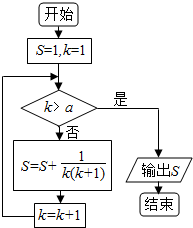
| A. | 13 | B. | 12 | C. | 11 | D. | 10 |
| A. | {0,2,4} | B. | {2,4} | C. | {0,3,4} | D. | {3,4} |
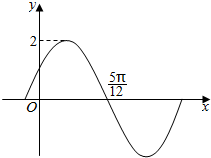 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,且f(0)=f($\frac{π}{3}$),则( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,且f(0)=f($\frac{π}{3}$),则( )| A. | f(x)的最小正周期为2π | B. | f(x)的图象关于直线x=$\frac{5π}{6}$对称 | ||
| C. | f($\frac{2π}{3}$)=-2 | D. | f(x)在[0,$\frac{π}{4}$]上是增函数 |
| A. | 5,10,15,20,25,30 | B. | 2,4,8,16,32,48 | ||
| C. | 5,15,25,35,45,55 | D. | 1,12,34,47,51,60 |
 如图所示的四面体OABC中,OA=OB=OC=a,∠AOB=90°,∠BOC=∠AOC=60°,点M,N分别是AB,OC的中点,点S是MN上靠近点N的三等分点.
如图所示的四面体OABC中,OA=OB=OC=a,∠AOB=90°,∠BOC=∠AOC=60°,点M,N分别是AB,OC的中点,点S是MN上靠近点N的三等分点.