题目内容
9.若变量x,y满足约束条件$\left\{\begin{array}{l}{x-1≥0}\\{2x-y-1≤0}\\{x+y-3≤0}\end{array}\right.$,则z=x-y的最小值为-1.分析 作出不等式组对应的平面区域,利用目标函数的几何意义,进行求最值即可.
解答  解:由z=x-y得y=x-z,作出不等式组约束条件$\left\{\begin{array}{l}{x-1≥0}\\{2x-y-1≤0}\\{x+y-3≤0}\end{array}\right.$,对应的平面区域如图(阴影部分)
解:由z=x-y得y=x-z,作出不等式组约束条件$\left\{\begin{array}{l}{x-1≥0}\\{2x-y-1≤0}\\{x+y-3≤0}\end{array}\right.$,对应的平面区域如图(阴影部分)
平移直线y=x-z,由图象可知当直线y=x-z,过点A点,
由$\left\{\begin{array}{l}{x=1}\\{x+y-3=0}\end{array}\right.$,可得A(1,2)时,直线y=x-z的截距最大,此时z最小,
∴目标函数z=x-y的最小值是-1.
故答案为:-1.
点评 本题主要考查线性规划的基本应用,利用目标函数的几何意义是解决问题的关键,利用数形结合是解决问题的基本方法.

练习册系列答案
相关题目
17.已知直线l1:x+ay-2=0,l2:x-ay-1=0,则“a=-1”是“l1⊥l2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.下列选项错误的是( )
| A. | 命题“若x≠1,则x2-3x+2≠0”的逆否命题是“若x2-3x+2=0,则x=1” | |
| B. | “x>2”是“x2-3x+2>0”的充分不必要条件 | |
| C. | 若命题“p:?x∈R,x2+x+1≠0”,则“¬p:?x0∈R,x02+x0+1=0” | |
| D. | 若“p∨q”为真命题,则p、q均为真命题 |
1.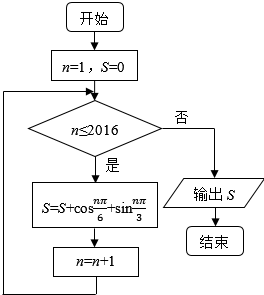 执行如图所示的程序框图,则输出结果S=( )
执行如图所示的程序框图,则输出结果S=( )
 执行如图所示的程序框图,则输出结果S=( )
执行如图所示的程序框图,则输出结果S=( )| A. | 0 | B. | -1 | C. | $\frac{1-\sqrt{3}}{2}$ | D. | $\frac{1+\sqrt{3}}{2}$ |
18.曲线y=ax+ex在点(0,1)处的切线方程为y=-x+1,则a=( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |