题目内容
函数f(x)=2cos(2x-θ+
)(0<θ<
)是偶函数.
(Ⅰ)求θ;
(Ⅱ)将函数y=f(x)的图象先纵坐标不变,横坐标缩短为原来的
倍,再向左平移
个单位,最后向上平移1个单位得到y=g(x)的图象,若关于x的方程g(x)-
-1=0在x∈[-
,
]有两个不同的根α,β,求实数m的取值范围及α+β的值.
| π |
| 6 |
| π |
| 2 |
(Ⅰ)求θ;
(Ⅱ)将函数y=f(x)的图象先纵坐标不变,横坐标缩短为原来的
| 2 |
| 3 |
| π |
| 18 |
| 2 |
| m |
| π |
| 6 |
| π |
| 6 |
考点:函数y=Asin(ωx+φ)的图象变换,余弦函数的图象
专题:三角函数的图像与性质
分析:(Ⅰ)根据f(x)是偶函数,且0<θ<
,求出θ的值;
(Ⅱ)由图象平移求出函数y=g(x)的解析式,再根据余弦函数的图象求出m的取值范围,利用反三角函数求出α、β的值,即可求α+β.
| π |
| 2 |
(Ⅱ)由图象平移求出函数y=g(x)的解析式,再根据余弦函数的图象求出m的取值范围,利用反三角函数求出α、β的值,即可求α+β.
解答:
解:(Ⅰ)∵f(x)=2cos(2x-θ+
)是偶函数,且0<θ<
,
∴θ=
;
(Ⅱ)由(Ⅰ)知,f(x)=2cos2x,
将函数y=f(x)的图象先纵坐标不变,横坐标缩短为原来的
倍,得y=2cos3x的图象;
再向左平移
个单位,得y=2cos3(x+
)=2cos(3x+
)的图象;
最后向上平移1个单位得y=2cos(3x+
)+1的图象;
∴y=g(x)=2cos(3x+
)+1;
又∵g(x)-
-1=0,
即2cos(3x+
)+1-
-1=0,
∴cos(3x+
)=
;
在x∈[-
,
]时,
3x+
∈[-
,
],
y=cos(3x+
)=
有两个不同的根α,β,
∴
≤
<1,
解得1<m≤2;
∴实数m的取值范围是(1,2];
又∵cos(3x+
)=
,
∴3x+
=arccos
,或-arccos
;
即α=-
+
arccos
,β=-
-
arc
;
∴α+β=-
.
| π |
| 6 |
| π |
| 2 |
∴θ=
| π |
| 6 |
(Ⅱ)由(Ⅰ)知,f(x)=2cos2x,
将函数y=f(x)的图象先纵坐标不变,横坐标缩短为原来的
| 2 |
| 3 |
再向左平移
| π |
| 18 |
| π |
| 18 |
| π |
| 6 |
最后向上平移1个单位得y=2cos(3x+
| π |
| 6 |
∴y=g(x)=2cos(3x+
| π |
| 6 |
又∵g(x)-
| 2 |
| m |
即2cos(3x+
| π |
| 6 |
| 2 |
| m |
∴cos(3x+
| π |
| 6 |
| 1 |
| m |
在x∈[-
| π |
| 6 |
| π |
| 6 |
3x+
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
y=cos(3x+
| π |
| 6 |
| 1 |
| m |
∴
| 1 |
| 2 |
| 1 |
| m |
解得1<m≤2;
∴实数m的取值范围是(1,2];
又∵cos(3x+
| π |
| 6 |
| 1 |
| m |
∴3x+
| π |
| 6 |
| 1 |
| m |
| 1 |
| m |
即α=-
| π |
| 18 |
| 1 |
| 3 |
| 1 |
| m |
| π |
| 18 |
| 1 |
| 3 |
| 1 |
| m |
∴α+β=-
| π |
| 9 |
点评:本题考查了三角函数的图象与性质的应用问题,也考查了由三角函数的值求角的问题,是中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
下列集合中,只有一个子集的集合为( )
| A、{x|x2≤0} |
| B、{x|x3≤0} |
| C、{x|x2<0} |
| D、{x|x3<0} |
已知M={x∈R|x≥2
},a=π,有下列四个式子:①a∈M;②{a}?M;③a⊆M;④{a}∩M=π,其中正确的是( )
| 2 |
| A、①② | B、①④ | C、②③ | D、①②④ |
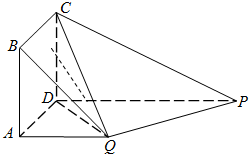 在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=
在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=